こんにちは、ゆるカピです。
今回は「引張と圧縮」について解説していきます。
- 応力とひずみにはどんな関係があるのか
- 構造力学ではどんな変形を考えるのか
- 軸剛性が高い低いはどうやって決まるのか
引張と圧縮は、構造力学の変形を考えるうえで最も基礎となる内容になります。
後に説明する予定の曲げモーメントにも関係する話なので、公式の丸暗記で理解があやふやな人は、この記事を読むことをおすすめします。

あやふやなところは早めに解決しておくといいよ。
フックの法則を振り返る
物体は力いっぱい引っ張ったり押し込んだりすると、伸びたり縮んだりします。
一般にこれをフックの法則といいます。
$$P = k \delta$$
力$P$はばねの剛性$k$とばねの伸び量$\delta$(デルタ)の掛け算で定義されています。
これについては第1回目の記事でも触れています。参考にどうぞ。
ばねの固さはどう決まっているの?

ばねには固いばねと柔らかいばねがあります。免震装置に使われるばねは人力では簡単に変形しませんが、シャープペンのなかにあるばねや子どもが遊んで使うレンボースプリングなどは手で簡単に変形します。
構造力学では、このような物体(ばね)の固さを剛性と呼んでいます。
それでは、先ほどのフックの法則の式だけで建物が設計できるかというと、そうはいきません。
それは、同じ材料であっても物体の形状(長さや太さなど)が変われば、ばねの伸び量$\delta$が変わってしまうからです。
そこで、材料ごとに表現しなおしたのが下式になります。
$$\sigma = E\varepsilon$$
$\sigma$(シグマ)は応力(曲げ応力、軸応力)、$E$はヤング係数、$\varepsilon$(イプシロン)はひずみを表しています。
このうち、ヤング係数は材料固有の係数となります。
つまり、材料から見た時、ばねの固さはヤング係数で決まることがわかります。
参考までに建築材料のヤング係数は以下のとおりです。
| 建築材料 | ヤング係数$[N/mm^2]$ |
|---|---|
| 鋼材 | 20,5000 |
| コンクリート | 21,000 |
| 等級E70のスギ | 6,800 |
なお、材料強度のばらつきはあるので参考程度としてください。
応力は「応力度」と表現されることがあります。例えば、法令集を開くと建築基準法では「許容応力度設計」と書かれていると思います。これは言い方の違いであって実務には影響しません。建築以外の分野では「応力」と呼ぶのが一般的らしいです。
ひずみはどう決まる?
物体の固さは、応力、ひずみ、ヤング係数によって決まることがわかりました。
そもそも、ひずみはどのように決まっているのでしょうか。
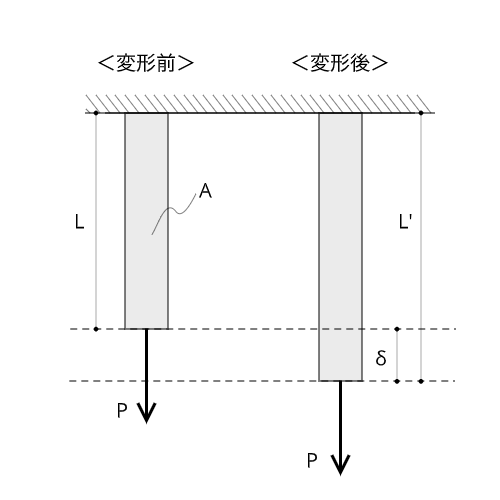
ひずみ$\varepsilon$は、元の長さ$L$を基準とする単位長さあたりの伸び量と定義されます。
これを聞いても、どういうこと?と疑問に思うでしょう。
例題で考えてみましょう。
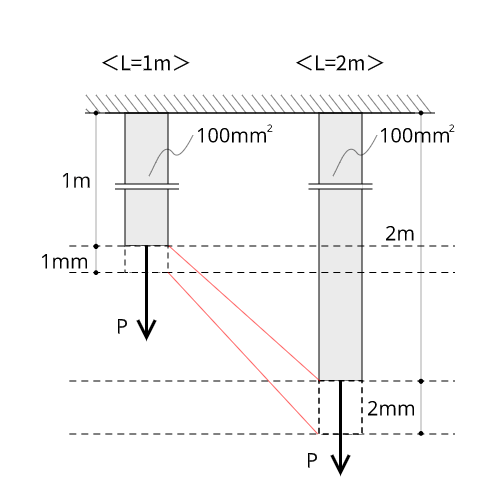
元の長さ$L$が1$m$、断面積$A$が100$mm^2$の棒があったとします。この棒の先端に10$kN$の力をかけた時、1$mm$だけ伸びました。では、長さが2$m$の場合はどれくらい伸びるでしょうか。
おそらく、あなたは直感的に1$m$が2倍の2$m$になるのだから2$mm$だろうと答えるでしょう。
つまり、元の長さ$L$を基準として比例的に計算できれば、どんな長さの部材でも伸び量$\delta$(デルタ)を計算することができるはずです。
伸びた後の長さを$L'$とすると、伸び量$\delta$は$\delta = L' - L$となります。
すると、ひずみ$\varepsilon$は
$$\varepsilon = \frac{L' - L}{L} = \frac{\delta}{L}$$
となります。
この式から、ひずみ$varepsilon$は元の長さ$L$に対する割合(比率)ということがわかります。
実際は伸びた分だけ断面積は小さくなりますが、その影響は微小なのでここでは無視しています。
変形の種類
物体の変形にはいくつか種類があります。
例えば、少年ジャンプのような分厚い雑誌を丸めるような変形と、両端を引っ張るような変形は違います。
また、ハサミのようにねじ切る変形も違います。
構造力学では主に4つの変形に分類しています。
- 軸変形
- せん断変形
- 曲げ変形
- ねじり変形
それぞれ、軸変形は軸剛性、せん断変形はせん断剛性、曲げ変形は曲げ剛性、ねじり変形はねじり剛性と対応しています。
このうち、建築士試験では軸剛性、曲げ剛性、せん断剛性の3つの剛性についての理解だけで十分です。
ねじり剛性は特殊な条件で適用されるのでここでは特に触れないこととします。
軸剛性と軸変形
この記事では、3つの剛性のうち、軸剛性と軸変形の関係について解説していきます。
軸変形は部材に引張力や圧縮力のみが作用する時の変形です。
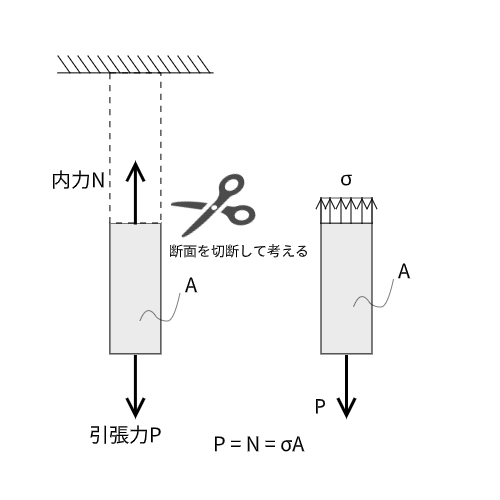
図のような棒の一部をとり出して考えてみましょう。
とり出した部分の切断面には内力$N$と呼ばれる力が作用しています。
これを切断面の断面積$A$で割った値を軸応力$\sigma$といいます。
$$\sigma = \frac{N}{A}$$
また、引張力$P$と内力$N$はつり合っているので、$P = N$となります。
これまで求めてきた式を組み合わせて引張力$P$と伸び量$\delta$を求めてみましょう。
$$P = N = \sigma A = E \varepsilon A = \frac{EA \delta}{L}$$
$P = k \delta$なので、
$$k = \frac{EA}{L}$$
と考えることもできます。この値$k$が軸剛性になります。
この式から、少ない力でたくさん変形させるためには、断面積$A$を小さく長さ$L$を長くなる、つまり、細長い部材にすればいいことがわかります。
逆に変形させたくなかったら、太くて短い部材にすればいいということです。
軸剛性のイメージはつかめましたか。
引張力を例に挙げましたが、圧縮力は引張力と反対の力なので、引張力を正(プラス)とすると圧縮力は負(マイナス)で表現すればOKです。
一般的には引張力を正としますが、圧縮力を正としても問題ありません。その場合は、正負の符号を間違えないように注意しましょう。
まとめ
お疲れ様でした。
今回は、4種類ある変形のうち、軸変形に注目して解説をしました。
剛性の話は一度に理解するのは大変な内容です。試験勉強で詰まった時の参考にしてみてください。
それでは、また。




































コメント
こちらのホームページを時々拝見しております。
本日閲覧したら、計算式のみがみんな文字化けしており、
こまっております。
他のホームページでは文字化けしていないようです。
対処いただけるとありがたいです。
ご指摘いただきありがとうございます。
いつも使っているプラグインのエラーだったようで、
先ほど修正しました。
また何かありましたらご連絡いただけると助かります。