こんにちは、ゆるカピ(@yurucapi_san)です。
あなたは3ヒンジラーメンの問題の解き方に悩んでいませんか。

力のつりあい式がうまく立てられない。

曲げモーメント図がうまく描けない。
部材の途中にヒンジ(ピン)があって支点がピン支点になっているラーメン構造のことを3ヒンジラーメンといいます。
今回は、知っていると案外簡単に解ける3ヒンジラーメンについて解説していきます。
今までの静定ラーメンとの違い

これまで学習してきた静定ラーメン構造は、支点がピンとローラーの組み合わせのものだけでした。
支点反力数が3つで、つり合い式も3つ立てられるから問題が解けていたというわけです。

静定ラーメン構造の基本の話は以下の記事で書いているよ。
ここで、支点が両方ともピン支点だったらどうでしょうか。
支点反力数が(鉛直・水平)× 2 = 4
となって問題が解けません。
そこで、部材の間に1つヒンジを付けてみたらどうでしょう。
ヒンジの部分を回転中心としたモーメントのつり合い式を1つ付け加えることができます。
これなら未知数4に対してつり合い式4となって問題が解けますね。
つまり、3ヒンジラーメンは静定構造ということがわかります。

そもそも静定構造ってなんだっけ?

そんな人は静定構造のことを解説している記事も目を通しておくといいかも。
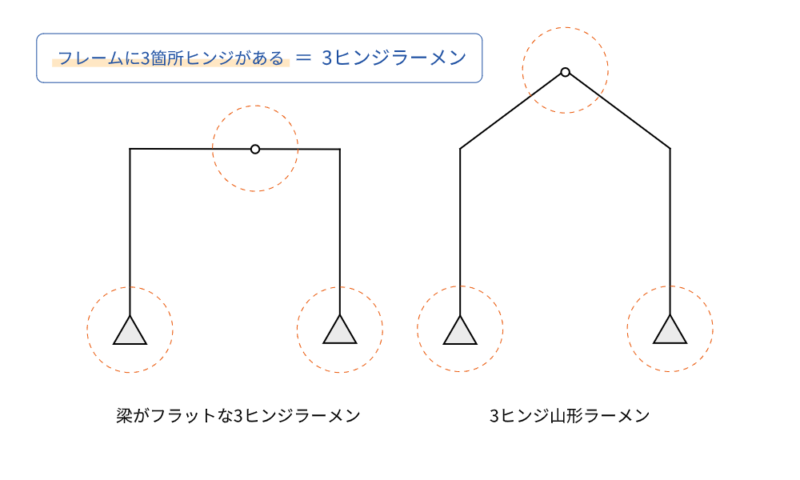
3ヒンジラーメンの種類
3ヒンジラーメンには、大きく梁がフラットなタイプと山形ラーメンのタイプの2種類あります。
3ヒンジ山形ラーメンの場合、頂部のヒンジを境に左右対称形になっているので片側のパーツを量産すれば作れてコストを下げられるメリットがあります。
3ヒンジラーメンの解き方

3ヒンジラーメンと聞いて特に身構える必要はありません。
実は解き方の基本はゲルバー梁と全く同じ。
ゲルバー梁のラーメン構造版という認識でOKです。
関連記事 »【構造力学の基礎】ゲルバー梁【第20回】の記事を読む
反力の求め方の3ステップ
3ヒンジラーメンの反力は次の3ステップで求められます。
- 鉛直・水平反力を設定してつり合い式を立てる
- ラーメン架構全体のモーメントのつり合い式を立てる
- ヒンジを境に左右に分割して、どちらかの自由体でモーメントのつり合い式を立てる
1と2は静定ラーメン構造と全く同じで、新しく3が追加されています。
この3ステップで反力が求められれば、後は静定ラーメン構造とまったく同じです。
解いていく流れは実例で解説したほうがわかりやすいので後述しますが、せん断力図から描き始めると簡単に曲げモーメント図を描くことができます。
詳しくは以下の「【裏ワザ】最速で曲げモーメント図を描く方法」という記事で解説しています。
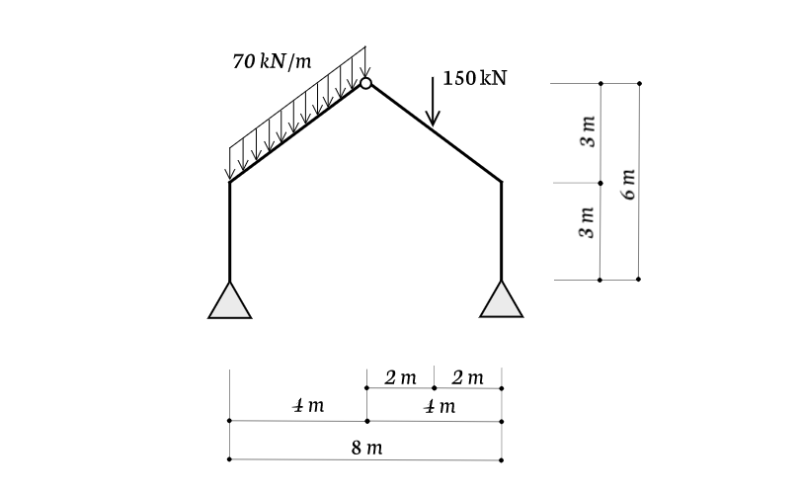
3ヒンジ山形ラーメンの問題を解いてみよう
おそらく3ヒンジ山形ラーメンの問題を解くのに困っていてこの記事を読んでいる人がほとんどだと思います。
なのでここでは3ヒンジ山形ラーメンの問題の解説をしていきます。
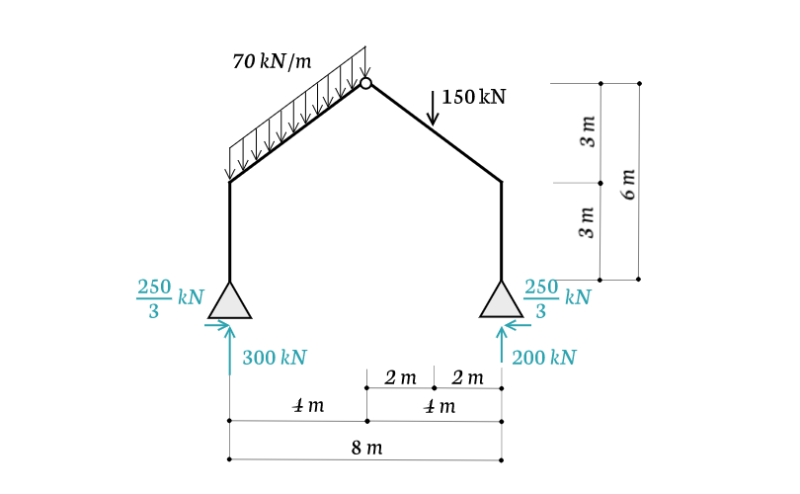
上図のような3ヒンジ山形ラーメンの問題を解いてみましょう。
反力を求める
解き方の流れはこんな感じで行います。
- 2つのピン支点に支点反力を設定する
- 力のつり合い式を立てる
- 折れている部分の$70 kN/m$の等分布荷重を集中荷重に直す
この時、掛ける長さは水平投影長さ$4 m$ではなく部材の長さ$5 m$であることに注意しましょう。

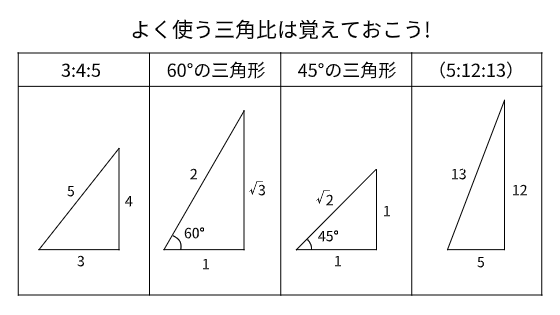
え、$5 m$?

$3:4:5$の三角比を思い出そう。よく使う三角比は覚えておくと便利だよ。
鉛直・水平・回転方向のつり合い式
力のつり合い式は次のようになります。
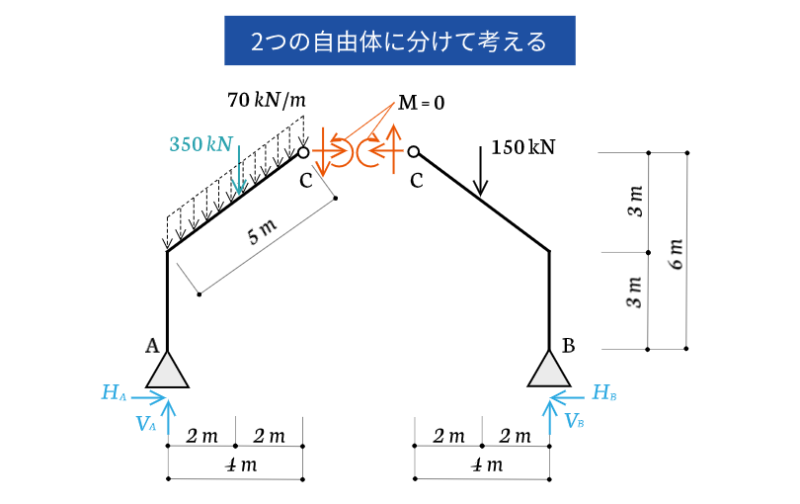
ここでのモーメントのつり合い式はラーメン架構全体で考えてください。
つり合い式の回転中心は点$A$としています。
$$V_A + V_B - 350 - 150 = 0$$
$$H_A - H_B = 0$$
$$350 \times 2 + 150 \times 6 - V_B \times 8 = 0$$
これらを解くと、$H_A = H_B , V_A = 300 kN , V_B = 200 kN$という答えが出てきます。
最後に$H_A$と$H_B$を求めるために、ヒンジ部分点$C$を回転中心としたモーメントのつり合い式を立てます。
ヒンジ部分点$C$を回転中心としたモーメントのつり合い式
今回は集中荷重のほうが式がごちゃごちゃしないので、右側の自由体図で考えます。
$V_B$は既に求められているので$200 kN$として計算します。
$$150 \times 2 + H_B \times 6 - 200 \times 4 = 0$$
これを解いて$H_A$と$H_B$を求めると、
$$H_A = H_B = \frac{250}{3} kN$$
となります。

これまで学習してきたラーメン構造と違って水平反力がゼロじゃないのがポイント。水平方向の外力がないからって水平反力がゼロということにはならないことに注意してね!
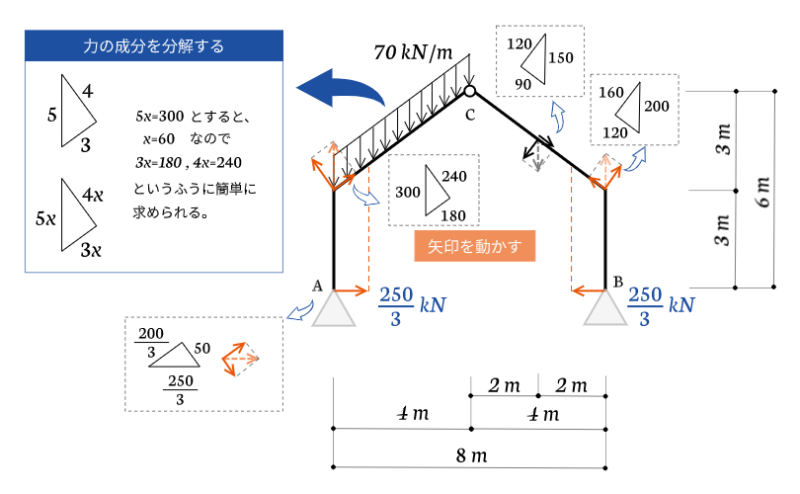
せん断力図を描く
求めた反力を記入すると上図のとおりになります。
この矢印符号を動かしながらせん断力図を描いていきます。
梁が斜めになっているため、支点反力を含め力の成分を分解しないと斜め部分のせん断力図が描けません。

これはちょっと面倒かも...。

通常のやり方で断面力の自由体から求める場合だったら、軸力Nとせん断力Qの連立方程式を解く必要があるよ。
慣れてないうちはどちらのやり方でも計算ミスしがちなので、どっちのやり方で解くかは好みが分かれそうですね。
結論、慣れたもん勝ちです。
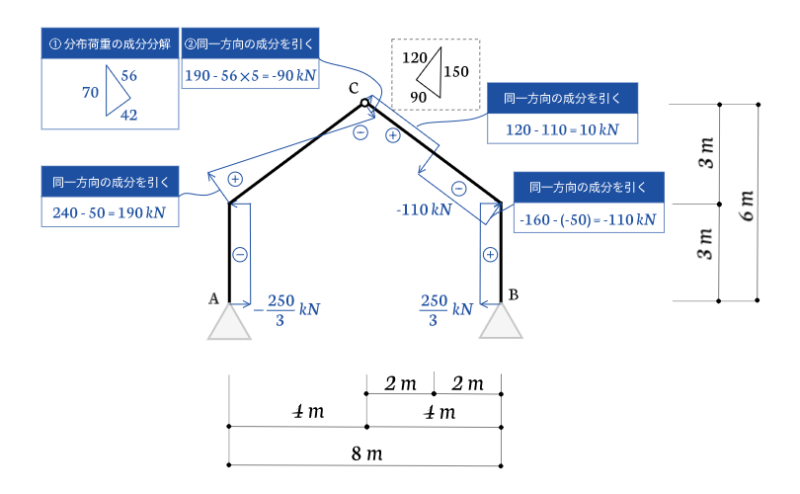
さて、これを整理して描くとせん断力図が完成します。
同一方向の成分の引き算を忘れないように注意しましょう。
力の分解をする時に、どっちが3でどっちが4なのか迷ったら、4のほうの辺の長さを長めに描くとわかりやすいです。
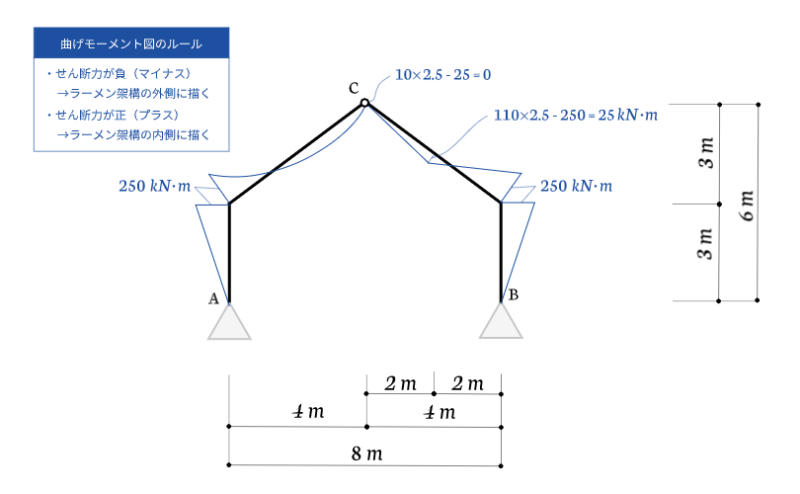
曲げモーメント図を描く
あと一息で終わります。

理解するのは難しいけど、何回も読み返してみるといいよ。
正直な話、せん断力を求めるのは大変ですが、残りの作業はそれほど大変ではありません。
せん断力図が描けていれば曲げモーメント図は簡単に描けます。
というのも、せん断力の大きさに長さを掛ければ曲げモーメントの大きさが求められるからですね。
まとめ
お疲れ様でした。
3ヒンジラーメンの問題が解ければ、ラーメン構造の問題は大丈夫でしょう。
バッチリ解けるという人は自信を持って大丈夫です。
いまいち解けないという人も、
- ヒンジを境にラーメン構造を分割して考える
- ヒンジを中心としたモーメントのつり合い式を立てる
この2つに気をつけて演習問題を解いていけば、いずれ解けるようになります。
以下、関連記事です。
復習したい人はこちらの記事もどうぞ。それでは、また。
Next» 【構造力学の基礎】梁の塑性崩壊【第22回】





































コメント