こんにちは、ゆるカピです。
今回のテーマは「断面力」です。
え、断面に力って、どういうこと？とあまり聞き慣れない単語かもしれません。
断面力は、これまで学習してきた軸力、せん断力、曲げモーメントを組み合わせた応力のことです。つまり、今まで学習してきたことの復習で理解できる内容です。
これをきちんと理解していないと、力学の大半の計算問題が解けません。大抵の場合、断面力のところで計算問題が解けなくて、そのまま苦手意識を持ってしまいます。
参考書や大学の講義で習ったけど、いまいち問題が解けないという人は、復習も兼ねてぜひ読んでみてください。
断面力の基本を理解しよう
断面力とは、軸力、せん断力、曲げモーメントを組み合わせた応力のことです。応力は内力ともいうので、断面力＝応力＝内力という認識でOKです。
実務では基本的に応力という単語しか使いません。というか、構造の本とか講義以外で聞く機会もありません。
用語の話は抜きにして、中身のルールをしっかり覚えておきましょう。
構造設計での役割
建築学生や構造の実務をしていない人からすると、断面力がどこで使うのかピンと来ないと思います。
構造設計では、建物の安全性を構造計算を通してチェックするわけですが、その内訳は、
- 建物にかかる外力や荷重を考える。（準備計算）
- 建物を構成する柱や梁などの部材に生じる断面力を求める。（応力計算）
- 部材に生じる断面力が部材の耐力以下に納まっているかを確認する。（断面計算）
というのが基本的な流れになっています。もちろん、これ以外でも計算しますが、最も基本となる部分がこの3つです。
このうち2つ目にあたるのが、今回取り上げている「断面力」です。つまり、断面力を求めないと建物が安全かどうか判断することはできません。
安全な建物を設計するために必要なプロセスだと覚えておいてください。
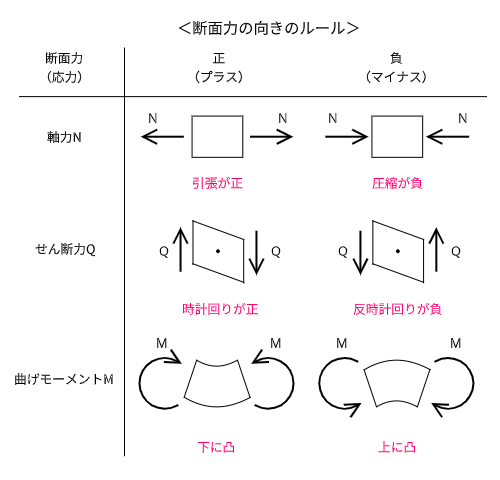
断面力の向きのルール
断面力には、力の向きのルールがあります。支点反力の時は自由に設定することができたのになぜ？と疑問に思うかもしれません。
その理由は断面力図を描く時にわかります。このルールを守っていないと、解答と全く違う断面力図を描いてしまうことになります。
人によって出てくる断面力図の形が違っていては、どれが正しいのか判断がつきません。このため、力の向きにルールをつけているのです。
断面力を間違える人で一番多いのは、向きのルールを守っていないことが原因だよ。このルールに早く慣れるためにもたくさん問題を解いてみよう。
ルールをわかりやすくするために、梁部材を基本として考えます。
- 軸力：引張方向（部材が伸びる方向）を正（プラス）とする
- せん断力：時計回りを正（プラス）とする
- 曲げモーメント：引張となる下側（凸形の変形）を正（プラス）とする
解き方の手順を理解しよう
断面力の求め方は次の手順で行います。ただし、この手順の前に必ず支点反力を求めることを忘れないようにしましょう。
- STEP 1自由体図を描く
- 部材をある点で切断する
- 部材の端から切断したある点までを描く
- STEP 2自由体図に荷重、外力、断面力を書く
- 部材の端から切断点までにある外力、断面力を書き込む
- 断面力の向きに注意する
- STEP 3力のつり合い式を立てる
- $\Sigma N = 0$
- $\Sigma Q = 0$
- $\Sigma M = 0$
の3つの式を作る
- STEP 4連立方程式を解く
- 力のつり合い式を解いて、断面力を求める
- STEP 5断面力図を描く
- 指定がなければ、描く優先順位はM→Q→Nの順
- 描き方のルールに注意する
STEP 1〜2：自由体図を描く
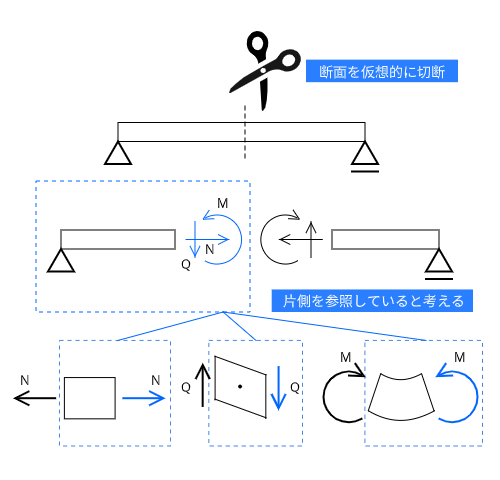
まず始めに、部材をある点で仮想的に切断すると考えます。実際に切断するわけではないので、切断面には断面力（内力）が生じます。
部材の端から切断したある点までを図で表現したものを自由体図といいます。自由体図に、該当している範囲にある外力（支点反力を含みます）と断面力を書き込みます。
この時、断面力の向きに気をつけましょう。切断した左側を描く場合と右側を描く場合で断面力の向きが反対になります。これは内力どうしもつり合っているからなのですが、なかなか間違えやすいところです。
慣れないうちは、切断した左側の場合で解くだけにするほうがいいでしょう。どちらを選んでも答えは同じになるので、多少時間がかかるにしても計算ミスをしないことを優先しましょう。
STEP 3〜4：力のつり合い式を立てる
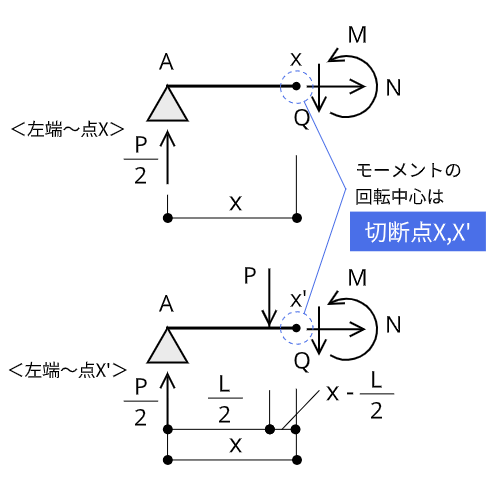
基本的に支点反力を求める時と同じやり方でできます。曲げモーメントのつり合い式だけ注意が必要です。回転中心を切断点にしないと、断面力のうち、未知数であるせん断力もつり合い式のなかに入ってしまって解けないためです。
切断点を回転中心にすると、せん断力が作用している点は切断点なので、せん断力の距離はゼロにできます。これで、曲げモーメントのつり合い式は、切断点の曲げモーメントと外力（支点反力を含みます）に距離を掛けたモーメントのつり合いだけで解けます。
STEP 5：断面力図を描く
断面力図には描き方のルールがあります。それぞれ、
- 曲げモーメント図（M図）は下側を正（プラス）として描く
- 軸力図（N図）、せん断力図（Q図）は上側を正（プラス）、下側を負（マイナス）で表現する
というものになります。
また、曲げモーメントとせん断力は微分・積分の関係となっているため、曲げモーメントの変化率がせん断力となっています。
曲げモーメント図が一次関数の直線になっていたら、せん断力図は横長の直線になります。二次関数の曲線だったら、せん断力図は一次関数の直線になっているはずです。
そうなっていなかったら、どこかで計算ミスをしています。必ず確認するようにしましょう。
実際に解いてみよう
それでは、早速問題を解いてみましょう。例題は、第8回の支点反力と同じ条件なので、反力は既に求められたという前提で進めます。
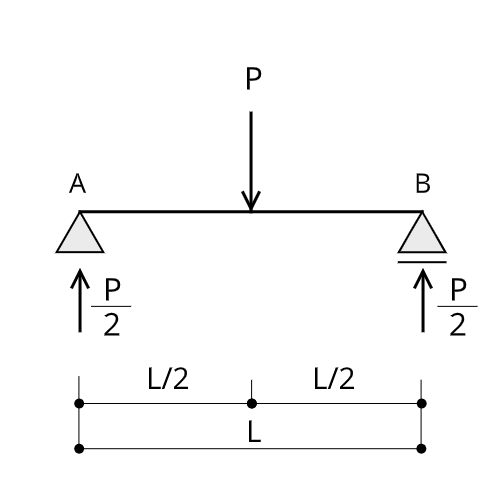
単純梁の例題
中央に集中荷重Pが作用したスパンLの単純梁について、手順に従って断面力を求めてみましょう。
自由体図を描く
まず、部材の左端から切断点X、X'までの自由体図を描きます。
力のつり合い式を立てる（端から外力Pの手前の位置Xまで）
- $\Sigma N = 0$
水平方向の力はかかっていないため、軸力Nはゼロです。
- $\Sigma Q = 0$
上向きを正として、
$$\frac{P}{2} - Q = 0$$
- $\Sigma M = 0$
X点を回転中心とし時計回りを正として、
$$\frac{P}{2} \times x - M = 0$$
これらの3つの連立方程式を解くと、
$$Q = \frac{P}{2} , M = \frac{Px}{2}$$
となります。$x = \frac{L}{2}$の時、$M = \frac{PL}{4}$です。
力のつり合い式を立てる（端から外力Pの先の位置X'まで）
- $\Sigma N = 0$
水平方向の力はかかっていないため、軸力Nはゼロです。
- $\Sigma Q = 0$
上向きを正として、
$$\frac{P}{2} - P - Q = 0$$
- $\Sigma M = 0$
X'点を回転中心とし時計回りを正として、
$$\frac{P}{2} \times x - P \times (x - \frac{L}{2} ) - M = 0$$
これらの3つの連立方程式を解くと、
$$Q = - \frac{P}{2} , M = - \frac{P}{2}x + \frac{PL}{2}$$
となります。$x = \frac{L}{2}$の時、$M = \frac{PL}{4}$となっているのを確認しておきましょう。
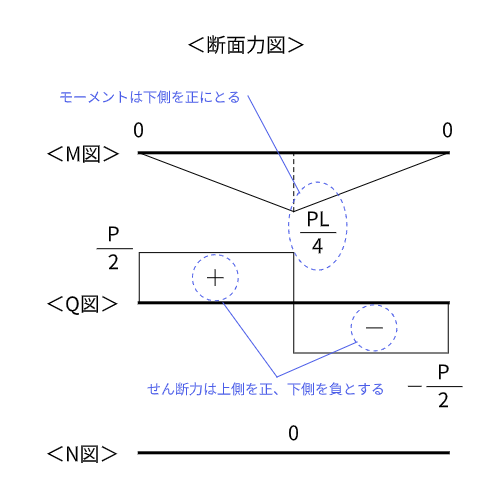
断面力図を描く
今回の問題では、部材の両端はピン支点とローラー支点なので、曲げモーメントは生じません。外力Pがかかっている中央の曲げモーメントの大きさがわかれば、後は直線で結んでやるだけで断面力図が描けます。
せん断力図は外力Pを境に正負が逆転するので、それを図に反映させます。
今回、軸力はゼロなので軸力図には"0"とだけ書きます。
まとめ
お疲れ様でした。
今回は断面力について例題を交えながら解説しました。
断面力の計算は習うより慣れよ、という格言にあるように、たくさん問題をこなして慣れてしまうのが、最もベターなやり方です。私自身、始めの頃は全くと言っていいほど、問題が解けませんでした。
最初のうちは解けなくても悔やむ必要はありません。たくさん間違えて復習して、の繰り返しで自然と身についてくるはずです。
軸力、せん断力、曲げモーメントの理解が不十分だなと感じた人は、以下の記事を参考にしてみてください。
計算の解き方がわかったからほかの問題にも挑戦したいという人はこちらの本で勉強するのもおすすめです。それでは、また。
コメント