こんにちは、ゆるカピ(@yurucapi_san)です。
今回は「分布荷重」について解説します。
- 構造設計実務歴7年目(組織設計事務所)
- 大学院時代に構造力学のTAを経験、ほか構造力学の指導経験あり
- 一級建築士試験ストレート合格

もっと詳しく知りたい人はこちらにもまとめています。
分布荷重というと、見た目からしてちょっと難しそうですよね。

矢印がいっぱいついていてなんか難しそう•••。
実際ここでつまづく人は少なくありません。
解けない人が一定数いるため、試験ではよく出題されるというわけです。
- 分布荷重と集中荷重の違い
- 分布荷重を使うタイミング
- 分布荷重→集中荷重の変換方法
分布荷重は、仕組みを理解してしまえば実はそれほど難しくありません。できないまま放置していたら問題作成者の思うツボです。
自分のものにしてライバルに差をつけましょう!
分布荷重はどんな荷重?
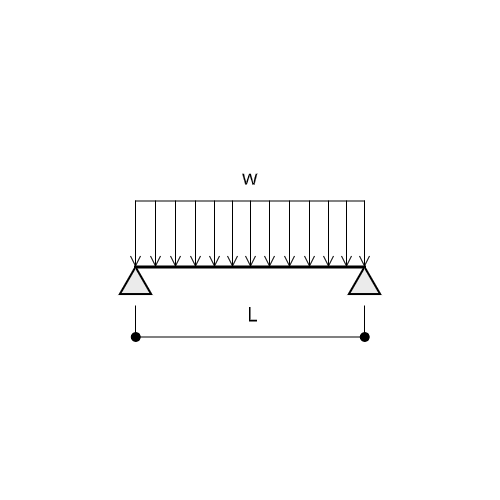
試験問題を解いていると、梁やラーメン架構に矢印がたくさんついているのをよく目にしますよね。
分布荷重は「単位長さあたりの荷重」を表しています。
単位は$kN/m$や$N/m$です。
また「単位面積あたりの荷重」もまた分布荷重のひとつ。単位は$kN/m^2$や$N/m^2$です。
では長さあたり(あるいは面積あたり)の荷重とはどんな荷重でしょうか?
いくつか例を挙げて考えてみましょう。
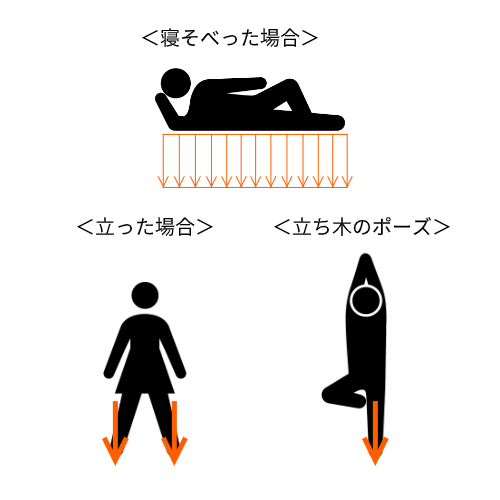
例1:人が寝そべった場合
床に大の字で寝転がっている時、体の体重は床に均等にかかっています。
体の一部だけに負担がかかっているということは、寝相が悪い場合を除いて、ないでしょう。
それでは、寝方を大の字から横向きに変えた時はどうでしょうか。
大の字で寝ていた時よりも体の片側の負担が増えたと感じるのではないでしょうか。
感覚的な話ですが、同じ重量がかかっても接地面の度合いによって、負担が違うことがわかります。
例2:人が立った場合
では、人が立っている場合はどうでしょうか。
この場合、両足に全体重がかかることになるため、両足の負担が大きいのは言うまでもありません。
片足で立ったら、爪先立ちしたら•••、さらに負担が大きいと感じるはずです。
このように、同じ重量でも接地面積が違うと体の負担は変わってきます。
これは床や梁などの構造駆体でも同じです。
重量に対して接地面積が大きい小さいの程度によって、力の分散具合が変わってくるということです。
構造力学の問題では、簡単に計算するために部材を奥行きのない平面的な線材に置き換えて計算します。
接地面積の大小で説明しましたが、単位長さあたりの分布荷重の場合は、奥行きの単位長さ1を既に掛けていると考えてください。
構造力学や設計実務ではこういうところで使う
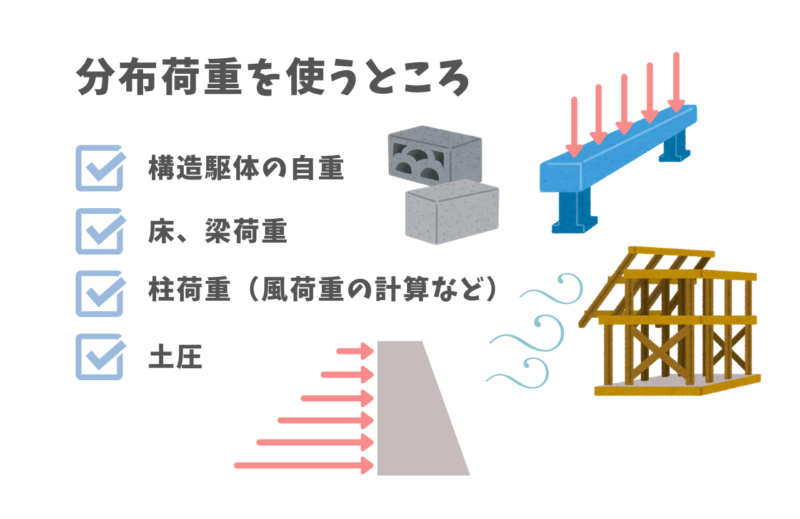
構造力学あるいは設計実務では、部材の計算を考える場合に分布荷重を使います。
- 構造駆体の自重
- 床、梁荷重
- 柱荷重(風荷重の計算など)
- 土圧
作用する荷重のばらつき具合によっては、一様に荷重が分布する等分布荷重だけでなく三角形分布荷重や台形分布荷重なども考える必要があります。
荷重の細かい使い分けについては話が長くなってしまうのでここでは説明を省きます。
分布荷重と集中荷重の違い
ここまで読んできて勘のいい人は、荷重の接地面積や接する長さによって分布荷重か集中荷重かが変わるのではないかと思うのではないでしょうか。
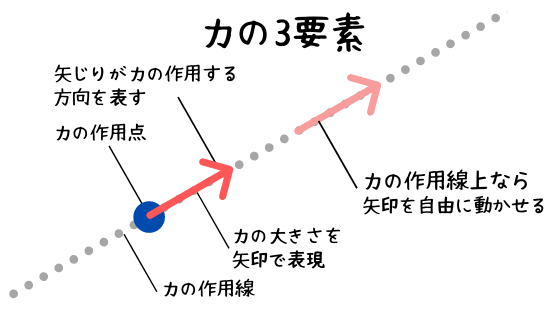
そもそも、第1回目の「力」では力には作用点がありそこからある方向に向けて力が作用すると説明しました。
集中荷重は「点荷重」となるのですが、実際世の中には接地面積ゼロの点で支えるものはありません。
この理屈でいくと、現実世界には集中荷重は存在しないことになります。
しかし、集中荷重という考え方はシンプルで非常に便利なので、概念的に集中荷重を使っています。
結局は設計者判断
では、分布荷重と集中荷重の使い分けの決め手はなんなのかというと、感覚的な違いしかないと答えるしかありません。
つまり、設計者判断、ということです。
梁部材全体に均一に荷重が作用していると考えれば、すぐに分布荷重だと判断できますが、実際にはきれいに荷重が作用することはほとんどありません。
集中荷重だと考える人もいれば、分布荷重で十分だと考える人もいます。
では、どうするか。
このあたりはケースバイケースですが、両方検証して間をとるという方法があります。
この方法だと独りよがりにならずに済みます。
いろんな人と合意をとる、というのは設計実務では非常に重要なことです。
どれくらい差が出る?
計算上、分布荷重と集中荷重とではどのくらい差が出るか検証してみましょう。
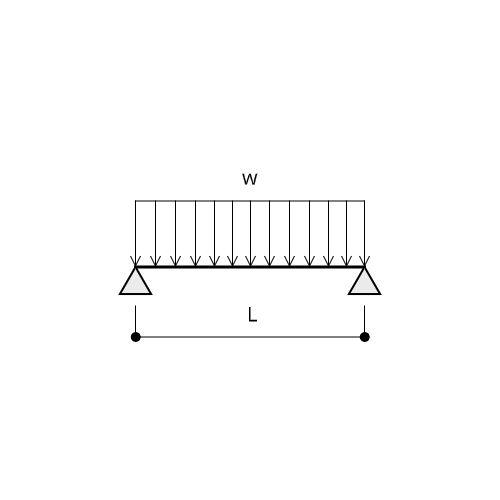
単純梁の場合
まずは単純梁から検証します。
・等分布荷重
$$M = \frac{wL^2}{8}$$
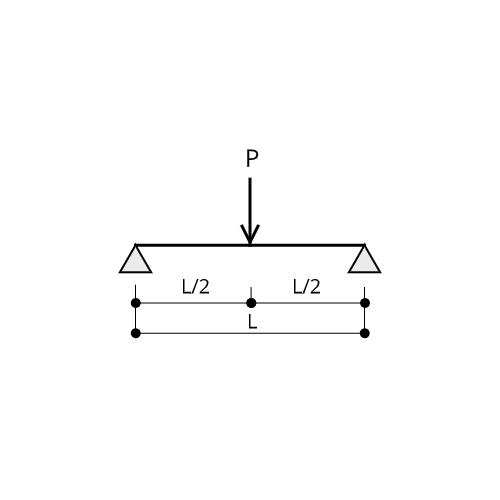
・集中荷重
$$M = \frac{PL}{4}$$
$P = wL$とすると、分布荷重と集中荷重とで2倍の開きがあることがわかります。
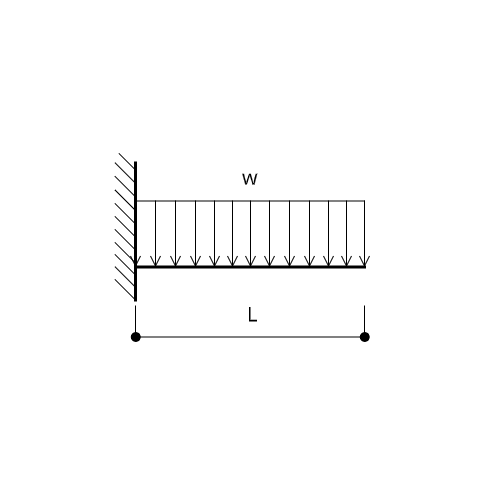
片持ち梁の場合
続いて、片持ち梁の場合はどうでしょうか。
・等分布荷重
$$M = PL$$
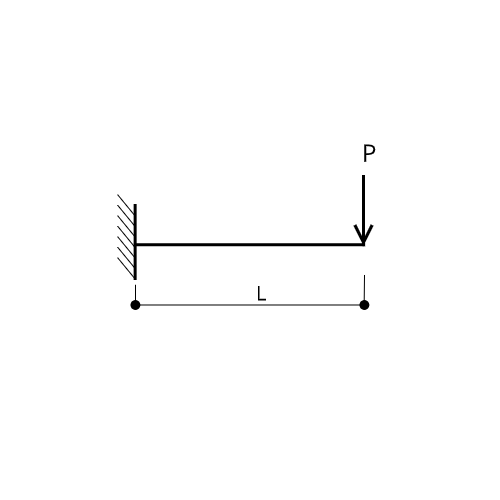
・集中荷重
$$M = \frac{wL^2}{2}$$
こちらも$P = wL$とすると2倍の開きがあることがわかります。
結構違いますよね。独りよがりな判断がいかに危険かがわかったと思います。

単純梁と片持ち梁とで4倍も開きがあるのも驚きだよね〜。
安全を意識しすぎるとコストがかかるし、経済性を優先しすぎると人命にかかわります。
荷重を考える時は、安全性と経済性のバランスが大事ということです。
分布荷重→集中荷重の変換方法
ここからは試験対策用の内容です。
分布荷重には等分布荷重のほかに三角形分布荷重や台形分布荷重などがあります。
試験では等分布荷重と三角形分布荷重がよく出題されます。
そのほかは出題されるかというと、求める方法が大変なので出題する側も出しづらいだろうから出ないと考えていいと思います。
この2つの荷重パターンについておさえておけば、とりあえずは安心ですね。
荷重分布形ごとにみてみる
等分布荷重と三角形分布荷重について、分布荷重→集中荷重への変換は次の手順で行います。
- STEP 1力の大きさを求める
「分布荷重」に「荷重が作用している範囲の長さ」を掛けると、集中荷重相当の力の大きさが出てきます。
- STEP 2分布形の重心の位置を求める
分布形を長方形や三角形の図形と同じようにとらえて、その図形の重心の位置を求めます。
- STEP 3力の大きさ、集中荷重の矢印、重心の位置をメモする
求めた力の大きさなどは、自由体図などの絵を描いて、後で見直しができるようにしておきましょう。
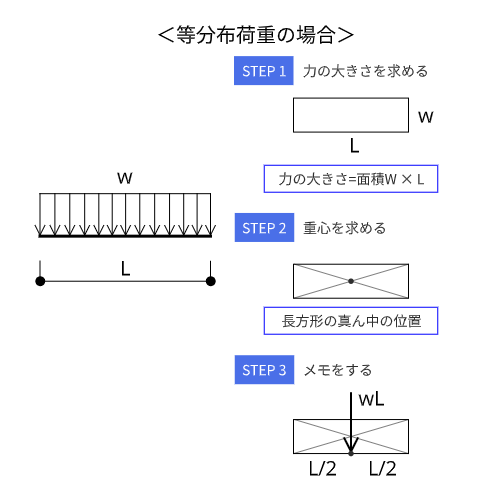
等分布荷重
等分布荷重の力の大きさは、分布形(長方形)の面積を計算すれば求められます。
重心の位置については、必ず中央にあるのでわかりやすいと思います。
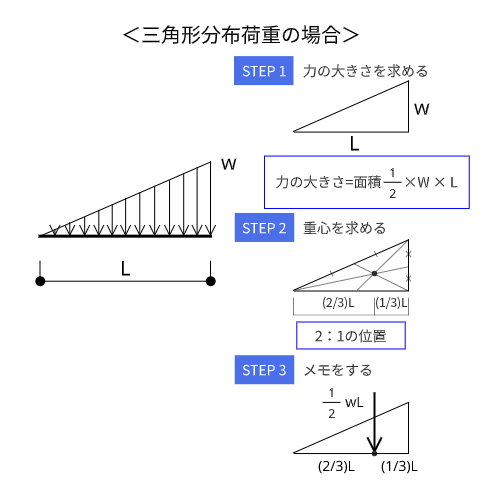
三角形分布荷重
三角形分布の場合も、同じように三角形の面積を計算すればOK。
少し厄介なのが重心の位置の求め方です。
計算する時間がもったいないので、2:1に内分する位置と覚えておきましょう。
まとめ
お疲れ様でした。
分布荷重の苦手意識は解消されたでしょうか。

え、解消できてないよ〜と焦る必要はなし!何度も読み直して復習してみて。
分布荷重の計算ミスをしてしまって、梁のたわみやラーメンの問題を間違えたという人は意外と多いです。
分布荷重→集中荷重への変換作業は計算の序盤にするので、途中でミスに気づいても直すのにもひと苦労します。
ミスを少しでも減らせるように入念にチェックしましょう。
計算に慣れてきたら構造力学も得点がぐんぐん伸びていきます。
ともに頑張りましょう。
それでは、また。



































コメント