こんにちは、ゆるカピ（@yurucapi_san）です。
先日、たわみ公式を使って不静定構造の問題を解く方法を解説する記事を書きました。
たわみ公式を使った問題はほかにもあって、よく水平剛性の問題として取り上げられることがあります。
この記事では、
- 前半：ラーメン構造の水平剛性の問題
- 後半：水平剛性を使った固有周期の問題
でお届けします。
水平剛性の問題の解き方がわからないという人の悩みの解決になれば幸いです。
それでは、早速始めたいと思います。
今回、ボリュームが多いから全部読むのはちょっと大変かも...。時間がある時に必要なとこだけ、読んで繰り返し学習することをおすすめするよ。
おさらい：力と変形の関係
本題の水平剛性の問題解説に入る前に、まずは力と変形の関係について簡単におさらいしたいと思います。力$F$と変形$d$の関係はフックの法則で表せます。
$$F = k d$$
これは力とたわみの関係でもあるので、たわみ公式を置き換えて考えることができます。有名な片持ち梁（梁の先端に集中荷重）の公式は、
$$\delta = \frac{PL^3}{3EI}$$
なので、これを$P$を左辺に持ってきて解き直すと、
$$P = \frac{3EI}{L^3} \delta$$
となります。先ほどのフックの式と見比べてみてください。$F$と$P$、$d$と$\delta$は同じものを表しているので、
$$k = \frac{3EI}{L^3}$$
となることがわかります。これが、今回扱う水平剛性のもとになる式です。
ラーメン構造の問題の解き方
ラーメン構造の水平剛性の問題を解くためのポイントは3点あります。
- ラーメン構造の梁を剛体として考える
- 部材端部の固定条件を理解する
- 1スパンのラーメン構造の水平剛性は柱の剛性の2倍で考える
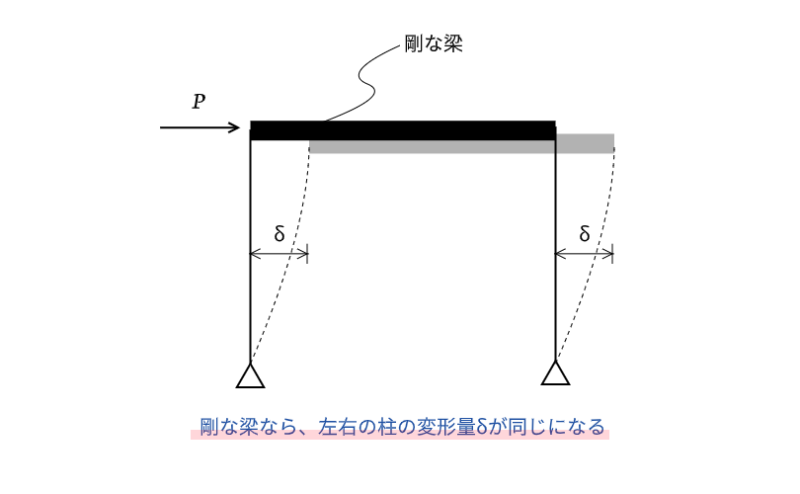
梁を剛体として考える
ラーメン構造の水平剛性の問題に出てくる梁は剛体で表現されています。剛体というのは伸び縮みしないで左から右（あるいは右から左）にそのまま力を伝える物体のことをいいます。
現実にはあり得ない話ですが、構造計算をする時に便利なので梁や床を剛体として扱うことがあります。床の場合は剛床といいます。
剛体じゃないと、左右の柱の水平方向の変形量がバラバラになって計算が複雑になってしまいます。梁を剛体とみなすことで、左右の柱の挙動が同じになりたわみの公式をそのまま当てはめることができます。
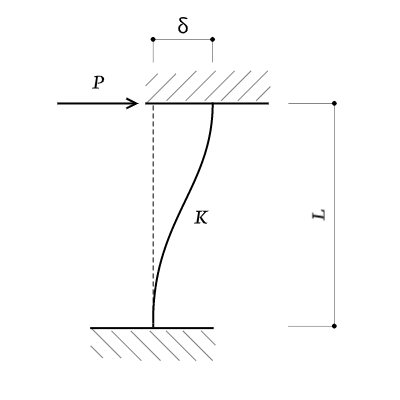
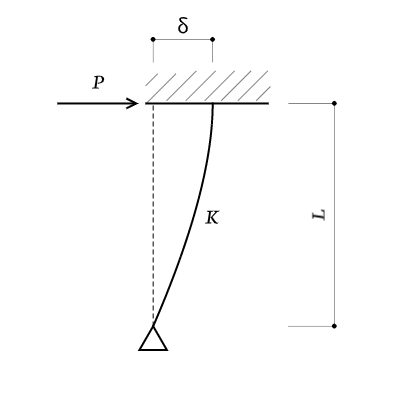
部材の固定条件を理解する
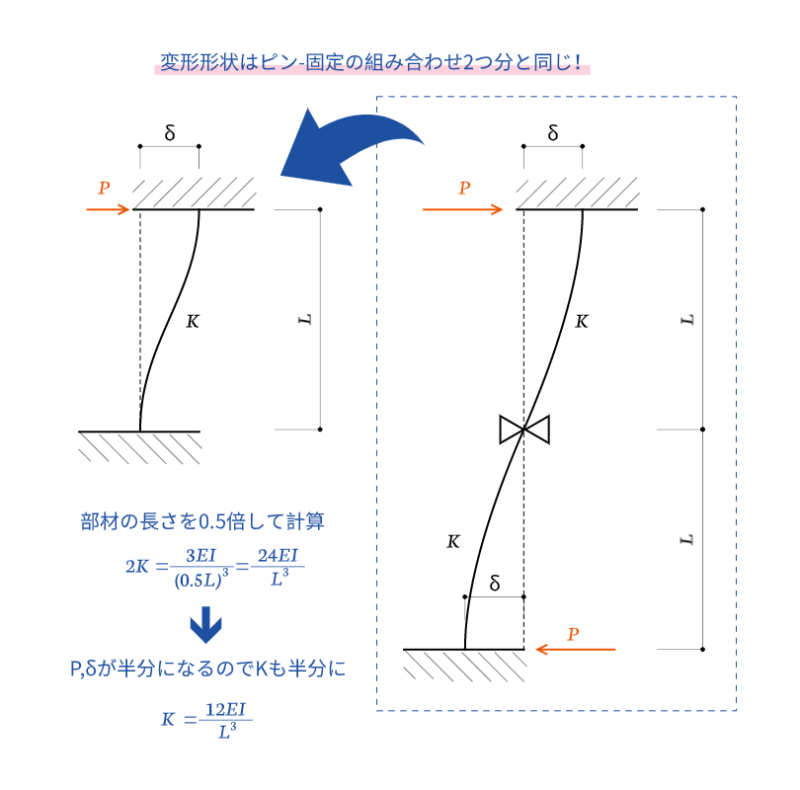
水平剛性の問題に出てくる部材の固定条件は、両端固定と、一端ピン他端固定の組み合わせだけです。それぞれ以下のような関係があります。
- 水平変位
$$\delta = \frac{L^3}{12EI} P$$
- 水平剛性
$$K = \frac{12EI}{L^3}$$
- 水平変位
$$\delta = \frac{L^3}{3EI} P$$
- 水平剛性
$$K = \frac{3EI}{L^3}$$
ちなみに、両端固定の組み合わせの変形形状は、ピン-固定の組み合わせの部材の変形形状を2つ合体させたものと同じなので、部材の長さを半分にして計算してから全体を半分に割れば、両端固定の組み合わせの水平剛性が求められます。
基本となる$\frac{PL^3}{3EI}$さえ覚えておけば楽チンだね。
1スパンのラーメン構造の水平剛性は柱の剛性の2倍
ここで注意しないといけないのが、先ほどの水平剛性の式が柱1本分を表しているということです。1スパンのラーメン構造であれば柱は左右に2本あるので、ラーメン構造全体の水平剛性は2倍する必要があります。
1スパンラーメン構造に置き換えると、下表のようになります。
- 水平変位
$$\delta = \frac{L^3}{24EI} P$$
- 水平剛性
$$K = \frac{24EI}{L^3}$$
- 水平変位
$$\delta = \frac{L^3}{6EI} P$$
- 水平剛性
$$K = \frac{6EI}{L^3}$$
いろいろなラーメン構造のタイプの比較の問題
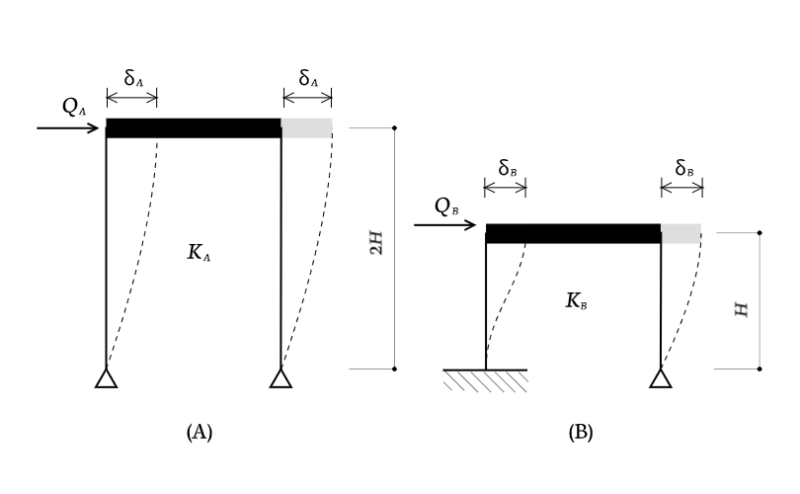
早速ですが、下図のようなラーメン構造の水平剛性$K$を求めてみましょう。
ちょっと意地悪に$(B)$の片側の支点だけ固定端にしてみました。剛な梁なので$\delta_B$は左右とも同じ大きさになります。
答えは次のとおりになります。
$$K_A = 2 \times \frac{3EI}{(2H)^3} = \frac{3EI}{4H^3}$$
$$K_B = \frac{12EI}{H^3} + \frac{3EI}{H^3} = \frac{15EI}{H^3}$$
$K_A$と$K_B$の比率は$1:20$になります。もし、$\delta_A = \delta_B$なら、
$$K_A : K_B = \frac{Q_A}{\delta_A} : \frac{Q_B}{\delta_B} = Q_A : Q_B$$
となり、$B$のフレームを$A$と同じだけ変形させるのに、$A$の20倍の力が必要になることがわかります。
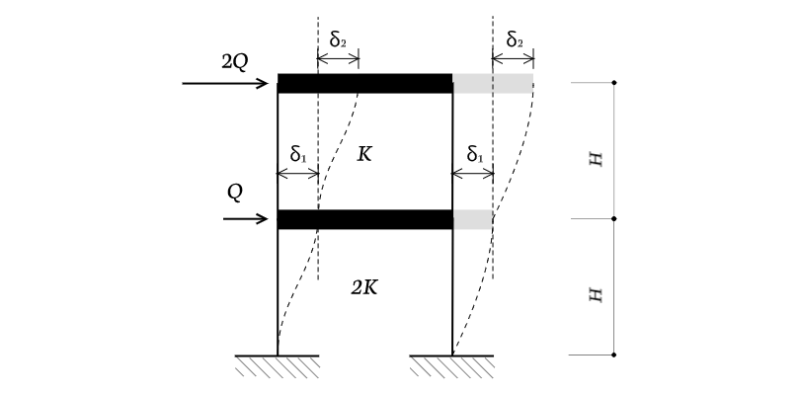
２層の層間変位の関係を問う問題
続いて、2層の層間変位$\delta_1$と$\delta_2$の比率を求めてみましょう。
今回は水平剛性があらかじめ設定されているので、各層の層間変位は層せん断力を各層の水平剛性で割ると求められます。
層せん断力は上図にある外力$2Q$や$Q$とは違います。「層」のせん断力なので、左右の柱のせん断力のことを差しています。
- 1層目：$2P + P = 3P$
- 2層目：$2P$
というように、違っているのがわかると思います。
ここはよく間違えやすいから気をつけよう！
計算すると、
$$\delta_1 = \frac{3P}{2K}$$
$$\delta_2 = \frac{2P}{K}$$
になります。$\delta_1$と$\delta_2$の比は、
$$\delta_1 : \delta_2 = \frac{3P}{2K} : \frac{2P}{K} = 3 : 4$$
となります。
建築の固有周期の問題の解き方
建築士試験では、ラーメン構造の問題のほかに建築の固有周期の問題でも水平剛性の知識が必要になります。
この手の問題は出題される要素が決まっているので、一度慣れてしまえば解きやすいタイプの問題です。以下のパラメータがあることを理解していればOKです。
- 固有周期を決定するパラメータ５種
- 部材端部の固定条件、計算パターン３種
げっ、こんなにパラメータがあるの？と思うかもしれませんが、
知らないと気づけない→解けない...。
知ってると公式に当てはめていける→解ける！
という感じで結果が大きく変わります。知ってると楽勝なのに、知らないばっかりに大損、なんてことになりかねません。なので、こういうパラメータがあるよ、というのは知っておいて損はないでしょう。
固有周期を決定するパラメータ5種
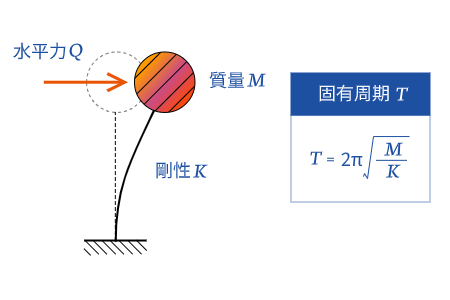
建築の固有周期$T$の公式は、建築の質量を$M$、剛性を$K$として、
$$T = 2 \pi \sqrt{\frac{M}{K}}$$
と表すことができます。これだけなら固有周期を決定するパラメータは$M$と$K$の2種類だけです。しかし、剛性$K$はたわみの公式を使って部材の長さ$L$、ヤング係数$E$、断面二次モーメント$I$に分解できます。
さらに、部材の断面が長方形なら、断面二次モーメント$I$は、
$$I = \frac{bd^3}{12}$$
となるので、さらに幅$b$とせい$d$が加わることになります。
まとめると、
- 質量$M$
- 部材の長さ$L$
- ヤング係数$E$
- 部材の幅$b$
- 部材のせい$d$
の5種類のパラメータになります。ヤング係数が異なる問題は今のところ見たことがないので実質4種類のパラメータに気をつけていればいいと思います。
部材端部の固定条件、計算パターンは３種
部材端部の固定条件や構造モデルによって解き方は決まっています。固定条件と計算パターンの組み合わせは次の3種類です。ラーメン構造の水平剛性は1スパンで考えています。
| 固定条件 | 構造モデル | 水平剛性 |
|---|---|---|
| (A)固定端+上部フリー | 1質点系モデル | $$K = \frac{3EI}{L^3}$$ |
| (B)固定端+剛な梁 | ラーメン構造 | $$K = \frac{24EI}{L^3}$$ |
| (C)ピン支点+剛な梁 | ラーメン構造 | $$K = \frac{6EI}{L^3}$$ |
例題でイメージをつかんでみよう
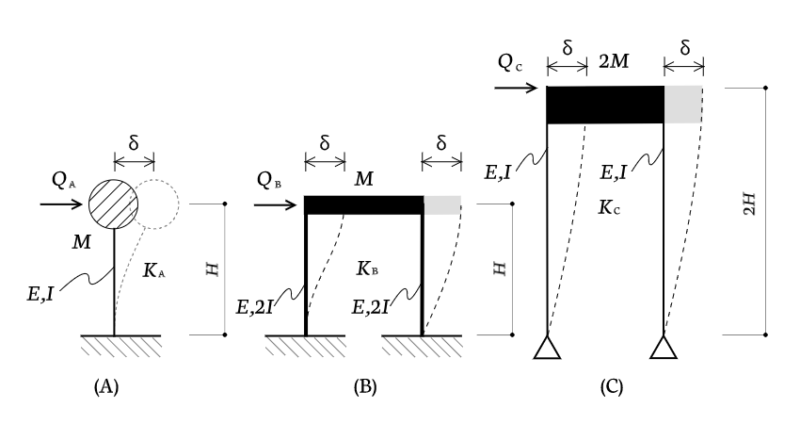
先ほど挙げた計算パターン3種を図で表現すると上のようになります。（質量$M$とか部材の長さ$H$とか、断面二次モーメント$I$とかは変えています。
(A)〜(C)に対応する固有周期の比を調べてみたいと思います。
まず、それぞれの水平剛性を求めます。答えは、
$$K_A = \frac{3EI}{H^3} , K_B = \frac{48EI}{H^3} , K_C = \frac{3EI}{4H^3}$$
となります。
比がわかればいいので、固有周期$T$のルートの中身$M$と$K$だけ取り出して比較します。ルート分の計算は後で行います。
$$T'_A : T'_B : T'_C = \frac{M}{K_A} : \frac{M}{K_B} : \frac{2M}{K_C}$$
$$= \frac{MH^3}{3EI} : \frac{MH^3}{48EI} : \frac{8MH^3}{3EI}$$
$$= \frac{1}{3} : \frac{1}{48} : \frac{8}{3} = 16 : 1 :128$$
よって、ルートを含めて比較すると、
$$T_A : T_B : T_C = 4 : 1 : 8 \sqrt{2}$$
となります。
いやあ、数式ばっかりで疲れちゃったよ〜。
いきなり理解するのは大変だし、何度か読み直してみることをおすすめするよ。
まとめ
今回は今までの集大成となる応用問題として、水平剛性の問題の解き方を解説しました。それぞれの単元の理解がちょっと不十分だったなという人は、関連記事があるので参考にしてみてください。それでは、また。
コメント