こんにちは、ゆるカピ(@yurucapi_san)です。
あなたはゲルバー梁の問題の解き方に悩んでいませんか。
構造力学の勉強をしていると一度は聞いたことがあると思います。建築を専門としていない一般の人なら、なんじゃそりゃ、ってなると思います。

ガリバーみたいなネーミングだね。ドラえもんのひみつ道具のガリバートンネルみたいな。入ったら小さくなったり大きくなったりするやつ。

考案したのがゲルバーっていうドイツの橋梁技術者だから、名前という意味では間違ってないかも...。
冗談はさておき、簡単に言うと連続梁の途中にピンのヒンジ(蝶番)がある梁のことです。
今回は、このゲルバー梁の仕組みと、具体的にどんな計算をしたらいいか解説します。
ゲルバー梁とは?

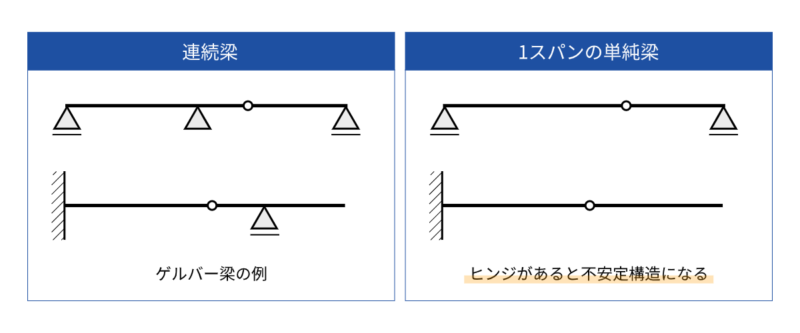
ゲルバー梁は連続梁の中間にヒンジ(ピン接合部)がある梁のことをいいます。ゲルバー梁には以下の特徴があります。
- ピン接合部の曲げモーメントはゼロ
- 問題として出題されるのは連続梁の場合のみ
- 単純梁と比較して、曲げ応力やたわみを抑えられる
計算を解くためには1つ目の知識は必須です。曲げモーメントがゼロになることを理解していないとそもそも問題が解けません。ピンの状態がいまいち理解できていないという人は支点、反力の記事を読んで復習してみてください。
2つ目については、問題を解くだけなら特に気にしなくてもいいかもしれません。なんで1スパンの単純梁の場合はないのかと疑問に思ったら、安定、不安定の記事を読むことをおすすめします。
連続梁の問題は不静定構造なので、つり合い式だけでは解けません。ゲルバー梁の場合は、ヒンジが梁の中間に1つ以上あり静定構造となるため、つり合い式だけで解くことができるわけです。
ゲルバー梁のイメージ

ゲルバー梁の元になっているのは、ゲルバー橋です。問題を解くだけならゲルバー梁の特徴をおさえるだけでいいかもしれませんが、いまいちイメージがつかみにくいのではないでしょうか。
なので、回り道になりますがゲルバー橋について簡単に説明したいと思います。
ゲルバー橋の特徴
ゲルバー橋は、2つの橋脚から張り出した片持ち部と、もう一方の片持ち部の間に新しく桁を載せることで大スパンを可能にした橋のことをいいます。
大きな河川に橋をかけるとなると、一番大変なのが橋の中央部分です。橋の中央は河川の水深が深く、建設コストもかさみます。また、洪水が発生したら濁流に押し流されるリスクが高いのも中央の部分です。
対岸からお互い張り出して建設すれば、経済的だしリスクも少なくなるというわけです。
また、お互い桁梁を持ち出しているため、ロングスパン梁にした場合に比べてたわみが少なくなるというメリットもあります。
ちなみに世界3大ゲルバー橋といえば、カナダのケベック橋、イギリス・スコットランドのフォース鉄道橋、大阪にある港大橋です。どれもかっこいいので、全部見てまわりたいですね〜。
ゲルバー橋のモデルは建築でも使う
ゲルバー橋の話を聞いて、それは土木の話であって建築は使わないんじゃないのと思うかもしれません。実際、大抵は梁の途中にヒンジなんて考えないで設計するので、あながち間違いではないでしょう。
しかし、それは鉄筋コンクリート造や鉄骨造の話。
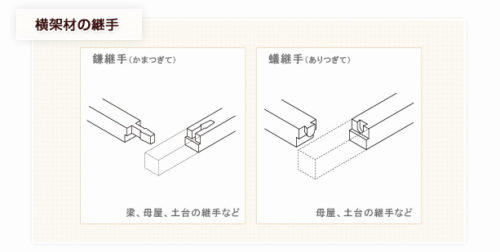
木造の在来軸組構法では継手部分も含めた梁で考える時は、継手部分をヒンジとしたモデルで考えます。これは、木造の継手が、鉄筋コンクリート造や鉄骨造と違ってガッチリと固定されないためです。
継手の位置取りが悪く、梁が不安定架構になっていたら要注意です。どうしてもその位置にしか配置できないなら、適切な補強が必要になります。
ゲルバー梁の解き方
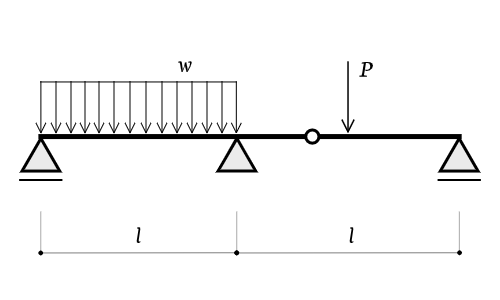
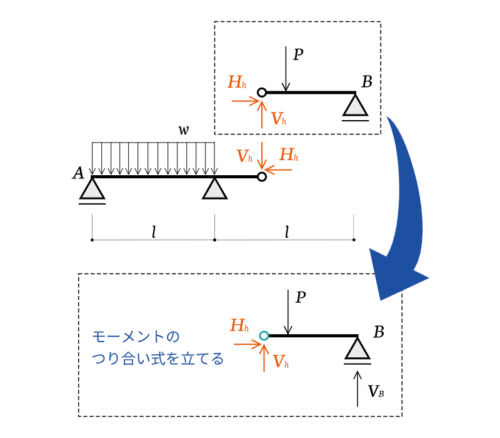
イメージの話はここまでにして、問題の解き方について解説します。図のような2スパンの連続梁で考えてみましょう。
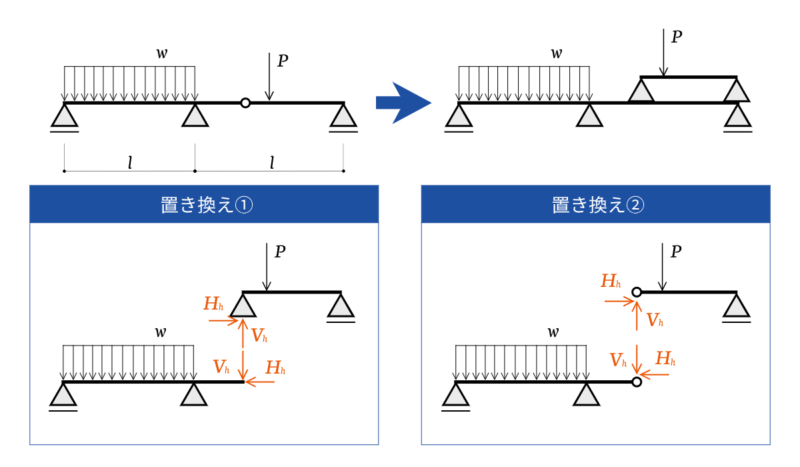
2つの静定梁に分割
ゲルバー梁は、ヒンジ部分を境に2つの静定梁に分割して考えることができます。この時注意したいのが、ヒンジの部分はピン支点と同じ動きをしないということです。
ゲルバー橋のイメージで考えると、ヒンジの部分から右側の梁は左側の梁に載っているだけです。支点ごと載っているので当然下にたわみます。
支点のイメージだとちょっと間違えそう、という人は端がピンの状態の2つの自由体ができたと考えてもいいと思います。
ヒンジ部分を回転中心とした力のつり合い式を立てる
分割した2つの静定梁についてそれぞれつり合い式を立ててもいいですが、ヒンジ部分を回転中心とした曲げモーメントのつり合い式を立てたほうが楽チンです。
ヒンジ部分に生じる鉛直、水平方向の力のやりとりを無視して計算できるためです。この解き方は3ヒンジラーメンという山形ラーメンの頂部にヒンジがあるラーメン構造の問題にも使えるので、ぜひ覚えておきましょう。
単純支持された張り出し梁との比較
ゲルバー梁が、単純梁と比較して曲げ応力やたわみを減らすことができるというのを実際に確認してみましょう。
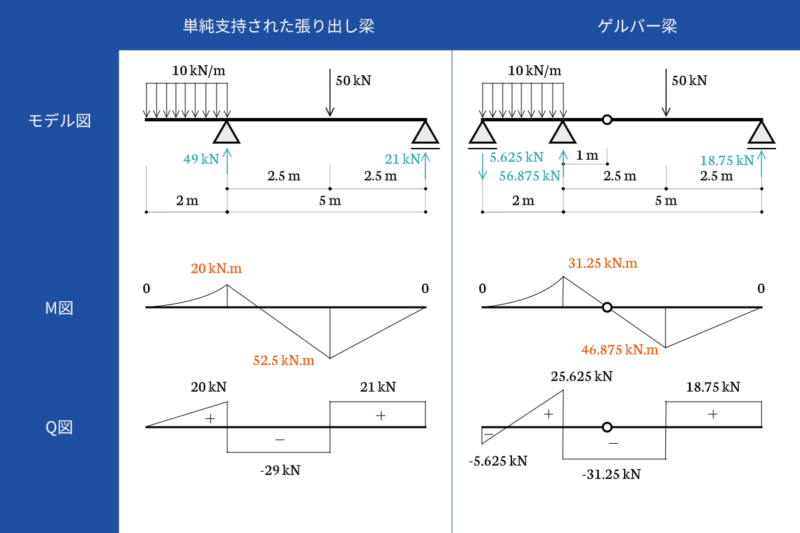
単純支持された張り出し梁とゲルバー梁とで曲げモーメント図を比較します。計算結果を比較したものが下の図です。

ゲルバー梁の反力、きれいな数字にならなかった(汗)。これはちょっと失敗しちゃったなあ...。
こんな難しそうな曲げモーメント図なんて、すぐ描けないよと思うかもしれません。実は細かい計算をしなくてもめちゃくちゃ速く描ける方法があります。
↓気になる人はこちらの記事をチェック!↓
梁の支え方によって応力の状態が変わる
支持条件の違いはありますが、ゲルバー梁のほうが5mスパンの最大曲げモーメントが小さくなっています。一方で、張り出し部分についてはゲルバー梁のほうが大きくなっています。
同じ部材断面で通して経済性と見た目の統一感を求めるなら、曲げモーメントの差が大きくないゲルバー梁のほうが良さそうです。
逆に、張り出し部分の先端を細く見せたいなら、左側の張り出し梁がいいかもしれません。
梁をどのように支えるかがポイントになるということです。
まとめ
お疲れ様でした。
ゲルバー梁のイメージはつかめたでしょうか。ヒンジ部分の曲げモーメントがゼロという考え方は3ヒンジラーメンの計算にも応用できます。ぜひマスターしてみてください。
問題の解き方がわかったから、もっと問題に挑戦したいという人はこちらの本が参考になります。それでは、また。




































コメント