こんにちは、ゆるカピです。
一級建築士試験の話になると、構造の計算問題が苦手、という意見をよく耳にします。もちろん、構造設計者だからよく聞かれるというのもありますが。
実際、計算というと暗記でなんとかならないし、学生の頃数学苦手だったし•••という感じで構造の計算も反射的に苦手意識を持つ人も少なくありません。
私自身、学生時代は構造はどちらかというと苦手でした。
構造の参考書は数式と難しい図ばかりで専門用語の羅列でよくわからない、と苦手意識を持っていました。しかも、試験用に勉強すれば要領よく問題が解けるのにそうしなかったせいで、テストの点もあまりよくありませんでした。
構造の問題をたくさんこなして、意外にも構造系の研究室に入り、大学院生時代は構造力学の内容を後輩に教えたりもしていました。
なので、みんなここで詰まるんだよなあ、というところがだいたい想像できます。
計算が苦手だという人は、苦手意識を克服するヒントにしてみてください。
力感覚がわかれば安全な建物が作れる
構造力学の基礎第1回目は、「力」について考えます。

「力学」だから当然といえば当然だけど、今回の話は試験問題を解くための必須の知識だよ。
おさらいも兼ねて力の考え方について見ていきましょう。
理論的な話
あなたは、ニュートン力学、あるいはフックの法則をご存知ですか?

高校の物理の授業で習ったやつだね。
ニュートン力学は3つ法則があって、このうち、第2法則では、
$$ma = F$$
と表現されています。力$F$は質量$m$とその運動の変化$a$(加速度)の掛け算で定義されます。
また、フックの法則では、
$$F = kd$$
と表現され、力$F$はばね$k$(物体の固さの程度)とばねの伸びd(変形量)の掛け算で定義されています。
感覚的な話
一方、先ほど挙げた力学の知識がなくても、私たちは普段の日常生活で力の伝達を経験しています。
例えば、人の歩行と自転車、トラックの重さやスピードの度合いによって、ぶつかった時の衝撃の違いを知っていると思います。
人にぶつかったくらいなら文句を言われる程度ですが、自動車による事故なら大惨事です。
また、金属(鉄やアルミなど)、木、衣服の繊維、ゴムなどの材料によって、力をかけた時の変形具合が違うということは誰もが知っていることです。
つまり、感覚的に経験的にこうだろうということを理論に当てはめたのが力学ということになります。
力学の知識を応用すれば、自分の身体スケールを超えた建物を建てることができるわけです。
構造設計者は数式ばっかり扱っているイメージをよくもたれますが、理論以上に感覚的なことや経験的なことを大事にしています。
普段から力の流れについて意識的に観察しておくことは、構造設計者に限らず大切なことです。
力の約束事
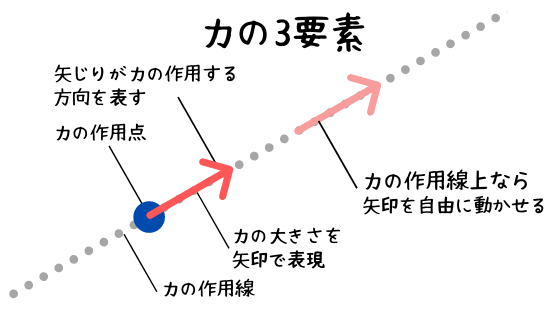
力学には約束事があります。力の3要素ともいえます。
- 大きさ
- 方向
- 力の作用点
試験問題を解く時にこれらの約束事を理解していないと、ケアレスミスをしてしまう可能性が高まります。
大きさ
力の大きさは矢印(↗︎)を使って表現します。
たまに矢印を書かず力の大きさの数字だけを書く人がいますが、どこにかかっている力なのか、後から見返した時に判断できなくなります。間違いのもとになるので、しっかりと矢印は書くようにしましょう。
方向
矢の先端を表す矢じりのほうをプラスにしたほうがわかりやすいです。
問題を解いていく過程で力の大きさがマイナスだった場合は、書き直して矢印を反対に数字をプラスにするか、矢印をそのままで数字をマイナスで表すかのいずれかとなります。
おすすめは前者です。
後で振り返った時にプラスに統一しておいたほうがわかりやすいためです。
書き直す時に矢印を書き間違えないように注意しましょう。
力の作用点
力が作用する位置のことを力の作用点といいます。矢じりのほうではないことに注意しましょう。
力の矢印が指す方向を線でなぞったものを力の作用線と呼びます。
力の作用線上であれば、形状や向きを変えなければ力の矢印は自由に動かすことができます。
この考え方はモーメントやトラスの計算などで役に立つので絶対に覚えておきましょう。
力のつり合い
ある力と同じ大きさの力が反対に作用すれば、全体で見た時、力はつり合っています。
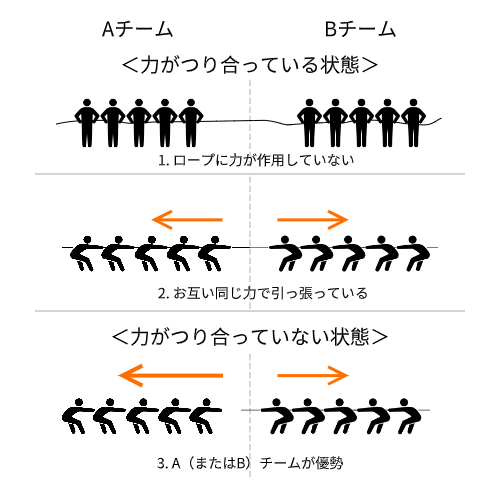
運動会などで行われる綱引きをイメージするとわかりやすいでしょう。
AチームとBチームそれぞれ5人ずつで綱引きをしたとします。この時、競技を始める前はお互い引っ張っていないため、力は作用せずつり合っています。
また、AチームとBチームがそれぞれ同じ力で引っ張り合えば、ロープは動かずに静止しています。この時も力はつり合っています。
では、力がつり合わない時はいつかというと、AチームかBチームのどちらかが優勢の場合です。
建物は、地震や台風などの一時的な力がかかっている時を除いて、静止しているのが通常です。なので、構造力学では力がつり合っている前提で計算します。
力$A$と力$B$が作用した時にその合計は、
$$A + B = 0$$
となります。
反力
物体の支持点に作用する力を表します。
支持点は、ピン、ローラー、完全固定に分類され、構造設計ではピンと完全固定の間にあたるばねを設定することもあります。
反力を設定する目的は、ある部材(あるいは建物)のモデル全体の力の流れを知りたい時に、その部材以外の力を除外して考えられるようにするためです。
例えば、建物のなかのひとつの梁部材に注目して力の流れを知りたい、という時に単純梁としてモデル化します。この時その梁の周りについている柱にかかる力は反力というかたちに置き換えて計算します。
反力に置き換えるメリットは、部材にかかる力の流れが単純化されてわかりやすくなることです。
単純明快な力の流れにしておくことで、誰から見ても安全な建物を設計することができます。
内力、外力
建物の内部に生じる力のことを内力、外側から作用する力のことを外力といいます。
ただし、一般的には内力は応力と呼んでいるので、ここでも今後は応力と表記するようにします。
外力は地震荷重や風荷重などの総称です。
これで部材の内部と外部それぞれに力を分解し、それぞれの力のつり合いを見ることができるようになります。
試験では、部材の内部の力のやり取りが理解できているかが重要になります。力を外部と内部で切り分けるという考え方をしっかり覚えておきましょう。
力の合成・分解
力は数学的にいうとベクトルなので、合成したり分解したりすることができます。
この時注意しないといけないのは、先ほどの力のつり合い式がそれぞれ同一の力の作用線上にないと使えないということです。
力を分解した結果が別々の力の作用線にあるものは、力のつり合いが成り立ちません。ここは試験問題を解いていてよく間違えやすいので注意しましょう。
よく使う三角比は覚えておこう
建築士試験では、トラス、斜めの部材を含んでいるラーメン、単純梁などの計算をする時に力の合成や分解を使います。
試験では小難しい三角関数の計算をする必要はありません。
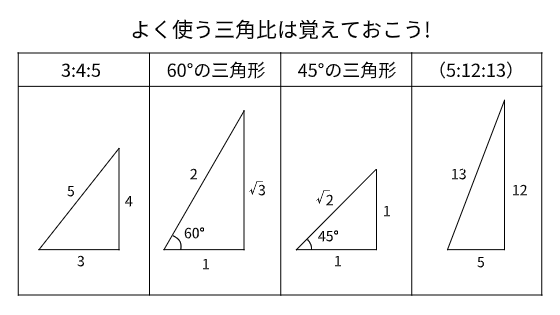
以下の3パターン(+おまけ1)の三角比だけを覚えておけば問題ありません。
- $3:4:5$の三角形
- 60°($1:2:\sqrt{ 3 }$)の三角形
- 45°($1:1:\sqrt{ 2 }$)の三角形
- (おまけ:$5:12:13$の三角形)
おまけは基本的に出題されません。理由は、かなり縦長か横長の形状になってしまい、部材モデルの現実味がなくなってしまうからかもしれません。
まとめ
以上で第1回目は終了です。お疲れ様でした。
今回は構造力学の基礎にあたる内容でしたが、ここの理解が不十分だとその後も大きなミスを犯してしまいます。
いま一度基本に立ち返ってみるのもいいでしょう。
それでは、また。



































コメント