こんにちは、ゆるカピ(@yurucapi_san)です。
今回はトラス構造の計算の基本である、節点法について解説していきます。
トラス構造の計算方法は、節点法と切断法(断面法)の2つです。このうち、今回お伝えする節点法は構造力学に慣れていない初心者向き、切断法は素早く効率よく問題を解きたい人向きの方法になります。
まずは、基本となる節点法について問題の解き方の解説をしたいと思います。
節点法の特徴
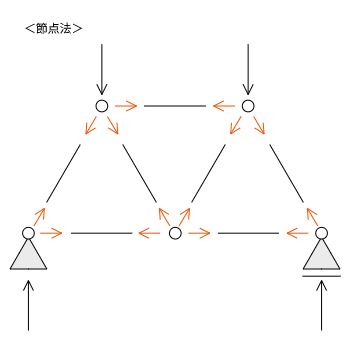
節点法は、節点にのみ外力や荷重が作用することに注目して、各節点での力のつり合い式からトラスの軸力を求めていく方法です。トラス構造の基本情報についてはこちらの記事をチェックしてみてください。
節点法を使うメリット・デメリットは以下のとおりです。
- 自由体図がわかりやすい
- つり合い式がシンプル
- 節点数が増えると計算が煩雑になる
- 必ず端部の節点からの計算になる
一番のメリットは、鉛直方向と水平方向だけのつり合い式で済むことです。モーメントのつり合い計算は間違えやすいので、構造力学が苦手な人でも、つまずかずに問題が解けます。
反面、節点数が増えるとその分だけ自由体図とつり合い式が増える方法なので、どうしても計算量が多くなってミスが出てきてしまいます。
また、支点反力や荷重が作用している端からしかつり合い式で計算できないのも大きなデメリットです。もし、トラス橋の中央部分の軸力を求めようと思ったら、端の支点反力位置から求める必要があります。
正直なところ、問題をこなしていくと、これらのデメリットが煩わしく感じてしまうと思います。トラス構造の問題にある程度慣れてきたら、より短時間で必要な軸力が求められる切断法に移行していくといいでしょう。
解き方の手順

節点法の解き方は次のとおりの手順で進めます。
- STEP 1支点反力を求める
- 支点反力のつり合い式を求める。
- STEP 2節点と部材に分解する
- トラスを節点と部材に分けた自由体図を描く。
- STEP 3各節点に生じる軸力を求める
- 鉛直方向、水平方向の力のつり合い式を立てる。
- つり合い式から軸力を求める。
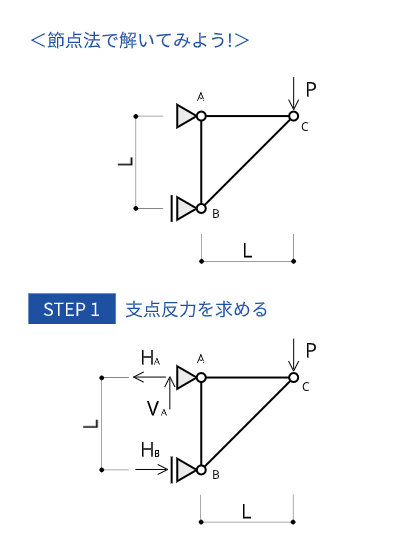
支点反力を求める
これはどの架構形式の計算問題でも共通ですね。
よく試験で出てくる問題は静定トラスなので、支点は基本的にピン支点とローラー支点の組み合わせになります。なので、トラス問題の反力計算は、単純梁の計算ができていればそれほど難しくはないと思います。
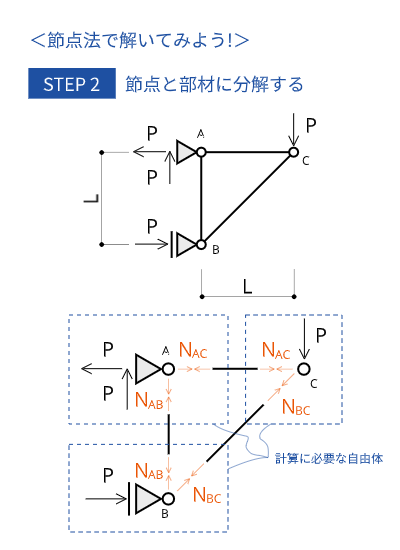
節点と部材に分解する
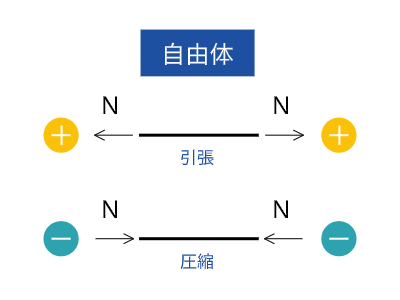
トラス構造の節点と部材を分けると上図のようになります。各節点にはそれぞれ引張軸力(内力)が生じていることがわかります。引張軸力を正(プラス)としているので、答えが負(マイナス)になれば矢印の向きが反対になります。
実は、ここが最も間違えやすいところです。
引張軸力の向きは、節点、部材ともに伸びる方向で考えます。もし、問題の図に直接軸力の矢印と大きさを描いてしまうとこの向きを間違えてしまうので、必ず自由体図を描くようにしましょう。

これをサボるとだいたい間違えるから、面倒でもちゃんと自由体図は描いたほうがいいよ。
また、自由体図はできるだけ大きく、トラス全体との関係がわかるように描いたほうが計算ミスを防げます。というのも、節点の数が多くなると計算途中でどの部分をとり出して描いたのかわからなくなってしまうからです。
無地の大きめのメモ用紙か方眼紙があると描きやすくて便利です。参考におすすめの方眼紙をリンクで貼っておきます。
各節点に生じる軸力を求める
鉛直方向、水平方向の力のつり合い式を立てて軸力を求めるのですが、ここで注意しないといけないのが軸力が斜めに生じているということです。
トラス構造の問題は必ず斜めの力が生じるので、力の分解をしっかりマスターしておく必要があります。
建築士試験に関しては、力の分解で必要になる三角比は図の左3パターンを覚えておけば大丈夫です。図の右端の5:12:13はスパンと高さの関係上、特に考える必要はありません。
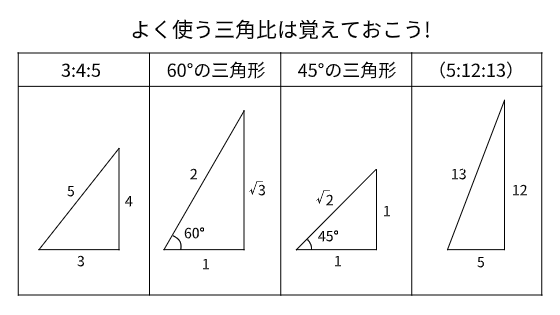
そうは言ってもこれをどう使ったらいいんだと思う人もいるかもしれません。サインとコサインはどっちがどうだったっけ?と迷う人にもおすすめの方法があります。
それは、全体に書かれている数字を三角形の斜辺に書いてある数字で割ってあげることです。例えば、3:4:5の三角形であれば、数字を5で割って数字の4と3のすぐ脇に$\frac{4}{5}$、$\frac{3}{5}$と書き込めば鉛直成分と水平成分がすぐにわかります。斜めの未知の軸力を$N$の場合は、さらに全体を$N$倍すればOKです。
例題を解いてみる

それでは、早速節点法で問題を解いてみましょう。例題では、最も単純な壁付けの棚のようなトラス構造を考えてみます。
支点反力を求める
支点にかかる鉛直反力および水平反力は力のつり合い式から求められます。
$$-H_A + H_B = 0 \Leftrightarrow H_A = H_B$$
$$V_A - P = 0 \Leftrightarrow V_A = P$$
$$H_A \times L - P \times L = 0 \Leftrightarrow H_A = P$$
これらの式をまとめると、$H_A = H_B = V_A = P$となります。
節点と部材に分解する
節点と部材に分解して自由体図を描くと下図のようになります。
今回は節点が3つ(点A,B,C)なので3つの自由体図が描けます。つり合い式は$2 \times 3 = 6$個です。トラスの三角形が増えるとつり合い式も増えるということです。
トラスの三角比は$1:1:\sqrt{2}$の45°の三角形で求めます。
節点Aの自由体
$$- P + N_{AC} = 0 \Leftrightarrow N_{AC} = P$$
$$P - N_{AB} = 0 \Leftrightarrow N_{AB} = P$$
節点Bの自由体
$$P + N_{BC} \times \frac{1}{\sqrt{2}} = 0 \Leftrightarrow \frac{N_{BC}}{\sqrt{2}} = - P \Leftrightarrow N_{BC} = - \sqrt{2} P$$
$$N_{AB} + N_{BC} \times \frac{1}{\sqrt{2}}= 0 \Leftrightarrow N_{AB} = - \frac{N_{BC}}{\sqrt{2}} = - ( - P ) = P$$
$N_{BC}$のように、分母のルートを有理化せずに残しておくと、$N_{AB}$の計算がしやすくなります。トラスの問題はこういうパターンが多いので、ぜひ覚えておきましょう。
節点Cの自由体
$$- N_{AC} - N_{BC} \times \frac{1}{\sqrt{2}} = 0 \Leftrightarrow N_{AC} = - \frac{N_{BC}}{\sqrt{2}} = - ( - P ) = P$$
$$- P - N_{BC} \times \frac{1}{\sqrt{2}}= 0 \Leftrightarrow \frac{N_{BC}}{\sqrt{2}} = - P \Leftrightarrow N_{BC} = - \sqrt{2} P$$
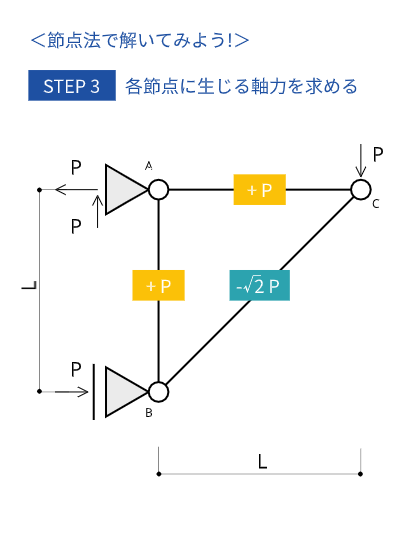
各節点に生じる軸力を求める
求めた軸力をまとめると図のようになります。
最後に、支点反力との関係が合っているか、上から外力$P$をかけた時に部材ABが引っ張られて、部材BCが圧縮されるような変形のイメージで合っているか、再度確認しましょう。
ここで変形のイメージと違っていたら計算を間違えている可能性があります。計算して終わりではなく確認作業もするように習慣をつけておくとミスを減らせます。
部材の変形量を求める
最後におまけで、部材の軸力による変形量を求めておきましょう。部材ACには引張力$P$が生じているので、部材のヤング係数を$E$、断面積を$A$として、部材ACの軸力による変形量$\delta$は、
$$\delta = \frac{PL}{EA}$$
となります。$P = 20 kN$、$L = 5 m$、$E = 205,000 N/mm^2$、$A = 3,000 mm^2$とすると、変形量$\delta$は約0.16mmになります。
軸力の公式を忘れてた、という人は下記に軸力についての記事があるので、参考にどうぞ。
まとめ
お疲れ様でした。
今回は節点法の解き方を解説しました。地味で面倒な作業をひたすらこなす計算法ですが、力のつり合い式だけで確実に点数がとれる方法です。私自身、構造力学が苦手な頃は、トラスの問題はなるべく節点法で解くようにしていました。
ただ、問題の難易度が上がるにつれて、考えないといけない節点の数が増えてくるので計算ミスはある程度避けられません。計算にある程度慣れてきたら、自転車の補助輪を外すような感じで切断法にも挑戦してみましょう。
まずは問題をたくさん解きたいという人にはこちらの本がおすすめです。私自身、学生の頃はこの本で勉強していました。量をこなして問題に慣れていきましょう。それでは、また。






































コメント