こんにちは、ゆるカピ(@yurucapi_san)です。
今回は、前回のラーメン構造の基本に続き、計算問題をどうといたらいいのかについて解説します。前回の基本の内容はこちらを参照ください。
支点反力や単純梁の断面力の問題は解けるという人が、次に解くのに苦労するのがこのラーメン構造の計算問題です。
そんな人の役に立てるように、よくつまずくポイントを中心に解き方の解説をしていきます。
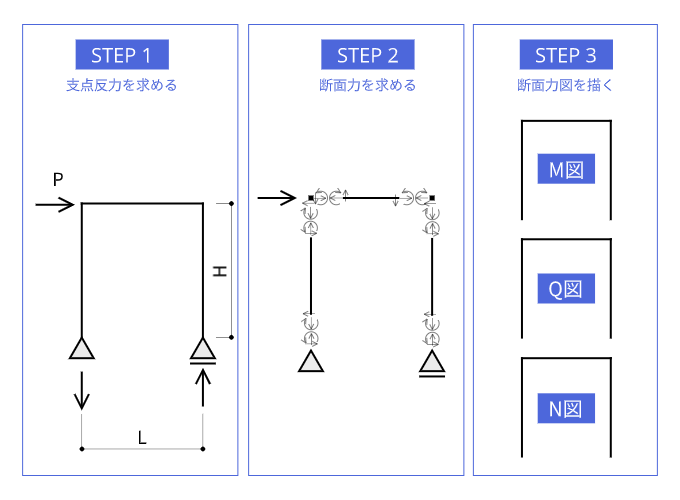
解き方の手順のおさらい

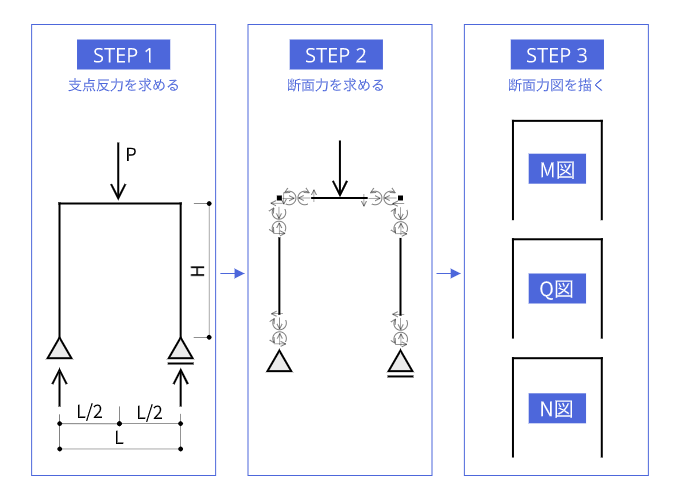
まず、問題の解き方の手順のおさらいをしたいと思います。計算問題を解く手順は以下のとおりです。
- STEP 1:支点反力を求める
- STEP 2:各部材の断面力を求める
- STEP 3:断面力図を描く
基本的には単純梁の場合と同じルールに従って解くのですが、ラーメン構造ならではの特徴もあるので注意が必要です。
つまずきやすいポイント
多くの人がつまずきやすいのが、
- 縦向きになったりL字形に曲がったりした場合の断面力の計算
- 門形になった場合の曲げモーメント図の表現方法
だと思います。私自身も始めの頃はここで苦労しました•••。
なので、このあたりを特に詳しく解説したいと思います。
単純支持ラーメン構造の計算例その1
早速、門形のラーメン構造についての問題を解いてみましょう。
支点反力を求める
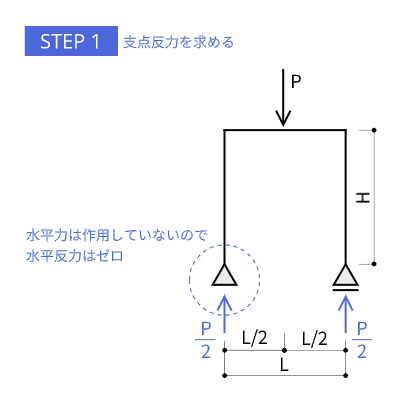
支点はピンとローラーのみなので、柱脚に曲げモーメントもモーメント荷重も生じません。また、外力は梁の中央に作用している$P$のみなので、鉛直方向の支点反力はそれぞれ等分されて$\frac{P}{2}$、水平反力はゼロとなります。
断面力を求める
断面力の計算をするうえで、重要なところをピックアップしてみました。
自由体図はいくつ描けばいいか
断面力は、自由体図を描いてつり合い式を立てて求めるのですが、ラーメン構造になると自由体図の数が急に増えて計算量が増えます。なるべく手間をかけずに断面力図を描くための断面力の情報を知りたいというのが本音ではないでしょうか。
自由体図を描き分けるポイントは、
- 切断する部材の前後に外力があるか
- 柱梁接合部などの部材の折れ曲がりがあるか
で決まります。
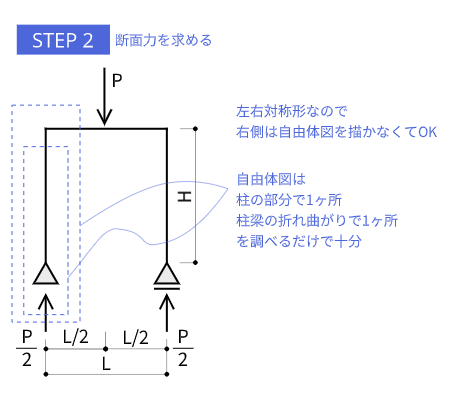
今回は、梁の中央に外力が作用しているのみで構造体としては左右対照なので、柱の部分で1ヶ所、柱梁の折れ曲がりで1ヶ所、の合計2ヶ所を調べるだけで断面力図が描けます。
外力を越えた先の梁の位置まで確認してもいいですが、外力の位置を境として曲げモーメントは減少するので左右対称だと考えれば計算は必要ありません。
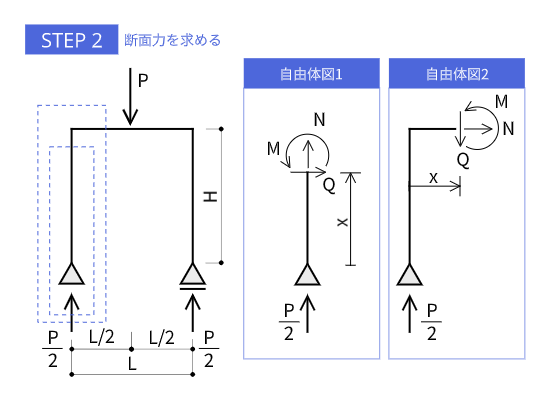
柱の部分の自由体図の描き方
柱の部分の描き方は、単純梁の場合を90°立てて起こしたイメージで描くだけです。単純梁の断面力の向きを間違えていなければちゃんと描けるはずです。
ちょっと怪しいなと思う人は、単純梁の断面力の向きを復習しておきましょう。
勘のいい人は、立てて起こして見た時、左側から見るか、右側から見るかで断面力の向きが変わってしまうのでは、と疑問に思うかもしれません。
結論から言うと、これはどちらから見てもOKです。
ただし、計算結果の数値どおりに曲げモーメント図を描くと正負が逆転してしまう可能性があります。門形ラーメンの曲げモーメント図を描く時は、あくまで曲げモーメント図の描き方のルールに従うようにしてください。
この問題の断面力は、つり合い式より、
$$N + \frac{P}{2} = 0 \Leftrightarrow N = - \frac{P}{2}$$
$$Q = 0$$
$$M = 0$$
となります。
梁の部分の自由体図の描き方
梁の部分の描き方は、自由体図としてはLを反転させたような形で描き、計算で使う任意の長さ$x$の位置を梁の端からスタートさせる、というのがポイントです。
任意の長さ$x$は支点からとってもいいのですが、計算が少し煩雑になってしまいミスしやすいので梁の端からスタートさせたほうがいいでしょう。
断面力の向きが再び90°回転することにも注意が必要です。
この問題の断面力は、つり合い式より、
$$N = 0$$
$$Q - \frac{P}{2} = 0 \Leftrightarrow Q = \frac{P}{2}$$
$$M - \frac{P}{2} \times x = 0 \Leftrightarrow M = \frac{P}{2} x$$
となります。$x = \frac{L}{2}$の時、$M = \frac{PL}{4}$です。
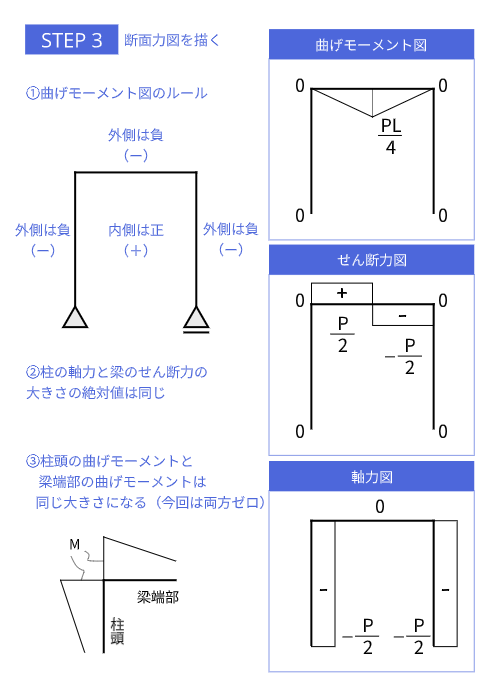
断面力図を描く
断面力図の特に曲げモーメント図には、門形の内側を正(プラス)、外側を負(マイナス)で表現するというルールがあります。これは単純梁の曲げモーメント図のルールと同じでたわみの変形と曲げモーメント図の形が合うようにするためです。
これによって、曲げモーメント図は荷重の位置に応じたパターン分けができます。あらかじめ曲げモーメント図の形がイメージできていれば、すぐに計算の間違いにも気づけるので、典型的なものは早めに覚えておくといいでしょう。
また、断面力図を描いてみると、軸力図とせん断力図の値に関係性があることに気づくと思います。これは、外力が梁のせん断力として柱に軸力として伝達して地面に伝達するということです。
もし、数値が合っていなければどこかで計算を間違えているということになるので、同じ値になっているか必ず確認しておきましょう。
実は、この問題は反力さえわかれば解ける問題です。どの問題でも通用するように解説しましたが、この問題に関して言うと水平反力がゼロなので、柱に生じる曲げモーメントもゼロになります。すると、剛節部分は柱と梁でつり合わないといけないので梁端部の曲げモーメントもゼロ。両端支持の単純梁の問題と同じになり公式から中央の曲げモーメントも求められます。
これを知っておくと計算しなくて済むので時間短縮になります。
単純支持ラーメン構造の計算例その2
続いて、横向きに水平力が作用した場合について考えてみましょう。
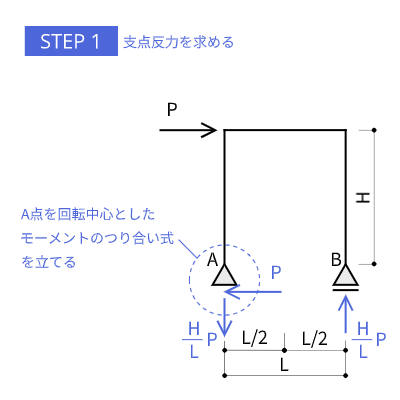
支点反力を求める
鉛直方向の外力は作用していませんが、水平力は作用しているため、抵抗するように上下方向の反力が生じます。A点を回転中心としたモーメントのつり合い式を立てると鉛直反力は、
$$V = \frac{H}{L} P$$
となります。水平反力は外力と同じ$P$がピン支点に生じます。
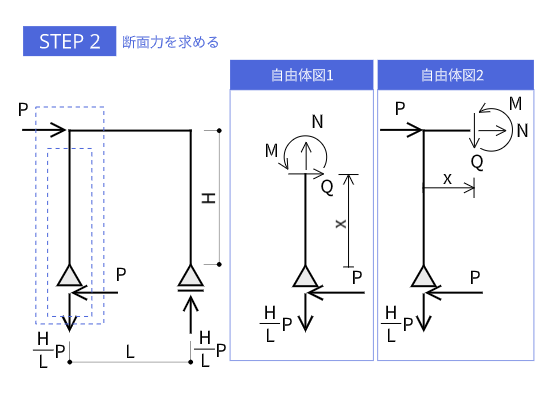
断面力を求める
水平力が生じた場合も自由体図の描く数は変わりません。柱の部分で1ヶ所、柱梁接合部分で1ヶ所描けばOKです。
柱および梁の部分の描き方は図のとおりになります。
それぞれの自由体図でつり合い式を立てます。
$$N = \frac{H}{L} P$$
$$Q = P$$
$$M =P x$$
となります。柱頭の位置での曲げモーメントは$M = PH$です。
$$N + P - P = 0 \Leftrightarrow N = 0$$
$$Q = - \frac{H}{L} P$$
$$M - PH + \frac{H}{L} P x = 0 \Leftrightarrow M = PH - \frac{PH}{L} x$$
となります。梁左端部の位置での曲げモーメントは$M = PH$、右端部の位置での曲げモーメントは$M = 0$であることがわかります。
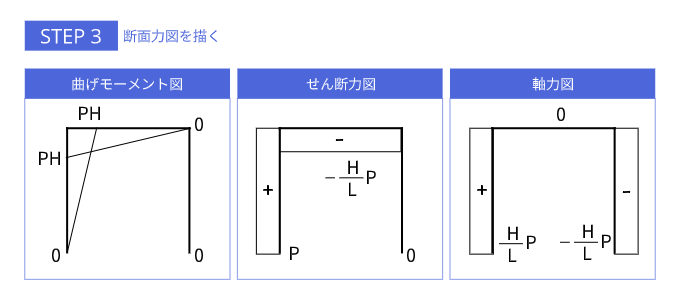
断面力図を描く
断面力図は図のようになります。
この問題に関しても、反力だけで断面力図が描けてしまいます。
支点はいずれもピンとローラーで、水平反力は1ヶ所のみなので柱に曲げモーメントが生じるのは左側だけだとわかります。右側の柱の曲げモーメントはゼロなので梁の右端の曲げモーメントもゼロ。後は左端の曲げモーメントと直線で結ぶだけで曲げモーメント図が完成します。
支点がピンとローラーの組み合わせになっている問題は、基本的に反力だけで解けます。ローラー支点は水平反力がゼロになるため曲げモーメントもゼロになるというのがポイントです。ぜひ覚えておきましょう。
まとめ
お疲れ様でした。
ラーメン構造の計算問題は作業量が多く計算ミスをしやすいです。問題に慣れないうちはたくさん間違えると思いますが、たくさん問題をこなして断面力図のパターンを覚えてしまうのが一番いい方法です。
建築士試験では正しい曲げモーメント図を選ぶだけという問題も過去に出題されているので、力の作用位置ごとの曲げモーメント図のパターンを覚えておけば、計算するまでもなく直感的に素早く解答を選ぶこともできるようになります。
計算の解き方がわかったからもっとたくさんの計算問題にチャレンジしたい、という人はこちらの本の問題を解いてみることをおすすめします。問題数は多いのでやり足りないということはないはずです。それでは、また。





































コメント