不静定構造をたわみ公式を使って解く方法を解説

不静定構造の問題は、つり合い式だけでは解けません。手計算で解く場合、たわみ角法や固定モーメント法、仮想仕事式などを使うのが一般的です。

でも、これらの計算って結構難しいんですよね。私自身、今でも間違える自信があります（笑えない...）。まあ、今はコンピュータを使って簡単に解ける時代だし、手計算と言ってもエクセルで組んで解くと思うので、あまり重要じゃない気がします。

じゃあ、不静定構造は建築士試験に出ないかというと、そんなことはないんですよ。

ゆるカピ

そう、残念ながら出るんだよね〜。

不静定構造のなかには、たわみ公式を使ってつり合い式プラスアルファで解ける問題があるんです。

今回は、たわみ公式を使った不静定構造の問題を解く方法を解説したいと思います。

ゆるカピ

知らなくても基本を理解していれば解けるから、「構造力学の基礎」からは外しています。最近よく出題されるから覚えておくと焦らなくて済むよ。

たわみ公式をおさらい

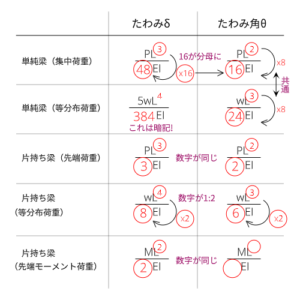
今回の問題を解くための大前提として、たわみ公式を覚えておく必要があります。よく出題されるたわみ、たわみ角の公式は以下のとおりです。

（クリックまたはタップすると拡大表示）

（クリックまたはタップすると拡大表示）

Aさん

うわぁ、覚えるのがいっぱいだぁ...。

全部覚えるのが大変という人も、まずは基本となる片持ち梁（先端荷重）の公式を覚えちゃいましょう！次に単純梁（集中荷重）を覚えるのをおすすめします。

たわみ、たわみ角については過去記事でも解説しています。

【構造力学の基礎】たわみ、たわみ角【第7回】

今回は「たわみとたわみ角」について解説していきます。 これまで力についてたくさん解説してきましたが、今回は変形の話になります。 先に言っておきますが、たわみ、たわみ角に関しては公式を暗記してしまったほうが早いです。 たわみ、たわみ角を真面目...

www.yurutto-kenchikulife.com

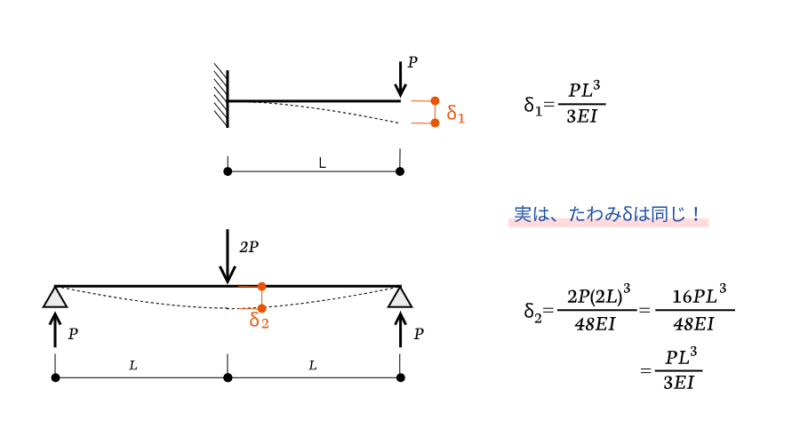
ちなみに、単純梁（集中荷重）のたわみは、片持ち梁（先端荷重）のたわみ公式の外力$P$を$P/2$、部材の長さ$L$を$L/2$とすると、求められます。これだけで覚える公式が減って楽になったのではないでしょうか。

このやり方は、分布荷重の場合は使えませんのでご注意ください。

解き方の手順

解き方は簡単で、今までの力のつり合い式にたわみの公式を付け加えるだけです。

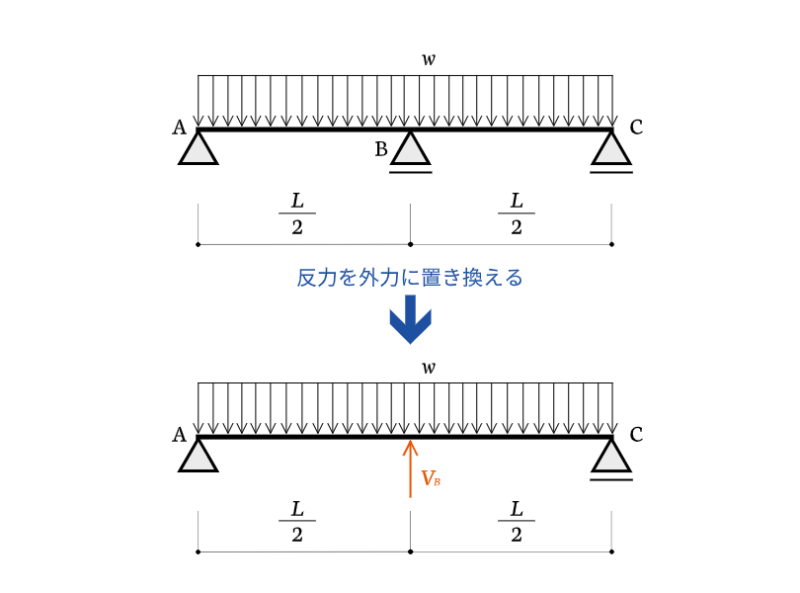
ほとんどの問題は、たわみ$\delta = 0$という式を使って解きます。典型的なのは以下のような連続梁の問題です。

この問題ではまず、点$B$の鉛直反力を外力$V_B$に置き換えるのがポイントです。支点反力は外力の一種なので置き換えても全く問題ありません。力のつり合い式に加えて、この点$B$の位置のたわみをゼロにする式を作ればOKです。

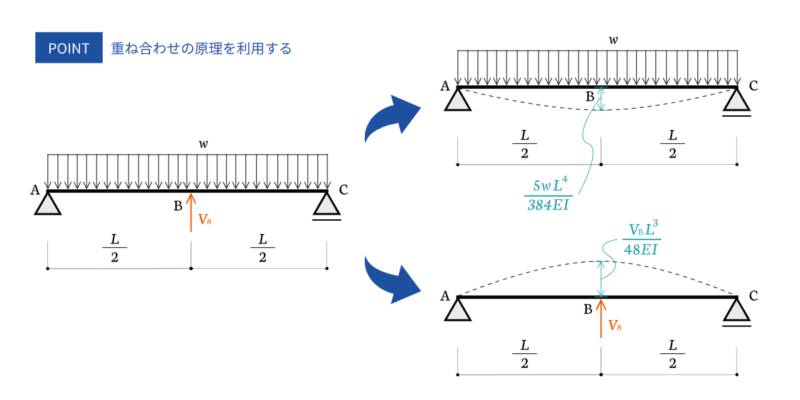
重ね合わせの原理を利用する

反力を外力に置き換えた時点の図を見てみると、外力が上下に作用しているせいで、たわみの公式がそのまま使えません。

こんな時は重ね合わせの原理を利用します。構造力学では、1つの梁の応力やたわみを2つの梁に分解して考えることができます。下図のようなイメージです。

点$B$のたわみはそれぞれ、

$$\delta_{B1} = \frac{5wL^4}{384EI} , \delta_{B2} = \frac{V_B L^3}{48EI}$$

となるので、この差がゼロになるように式を立てます。

$$\delta_{B1} - \delta_{B2} = 0 \leftrightarrow \frac{5wL^4}{384EI} - \frac{V_B L^3}{48EI} = 0$$

これを解くと、

$$V_B = \frac{5}{8} wL$$

という答えが出てきます。あとは左右対称系なので、全体の外力から$V_B$を引けばほかの支点反力も求められます。

$$H_A = 0 , V_A = V_C = \frac{3}{16} wL , V_B = \frac{5}{8} wL$$

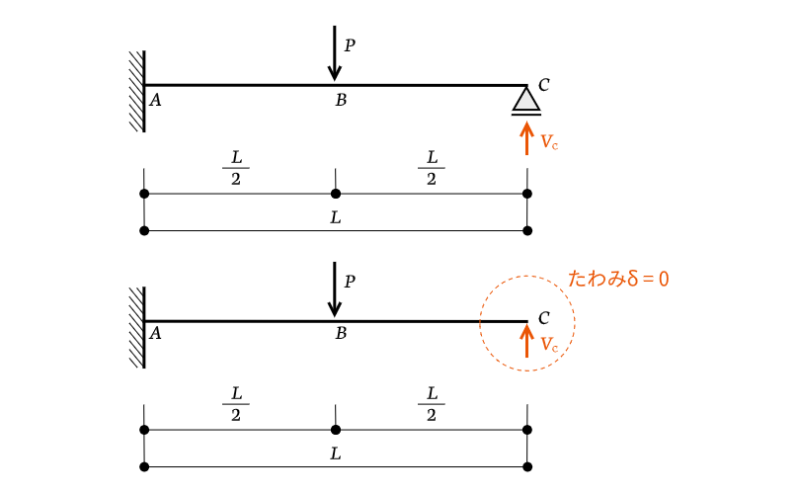
問題例：片持ち梁

片持ち梁の問題でも考えてみましょう。

今回の場合は、梁先端部分$C$のたわみをゼロにすればOKです。ただし、外力$P$が梁の中間に作用しているので、重ね合わせの原理で考える部材の長さには注意が必要です。

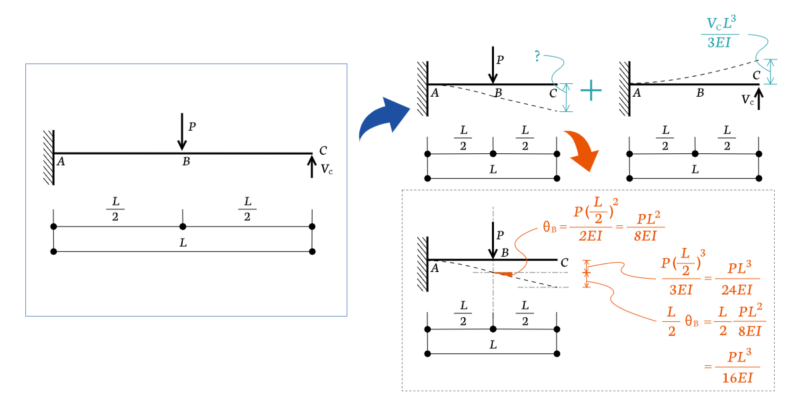
たわみ角の公式を利用する

重ね合わせの原理で分けると下図の右側のようになります。

点$C$のたわみは点$B$のたわみだけでは求められません。点$B$のたわみ角を使って求める必要があります。というのも、外力$P$が作用しているほうの梁は、点$B$より右側には力が作用せず変形が直線的になるからです。

つまり、点$C$のたわみは、

$$\delta_{C1} = \frac{PL^3}{24EI} + \frac{PL^3}{16EI} = \frac{5PL^3}{48EI}$$

$$\delta_{C2} = \frac{V_C L^3}{3EI}$$

$$\delta_{C1} - \delta_{C2} = 0$$

なので、

$$V_C = \frac{5}{16} P$$

となります。

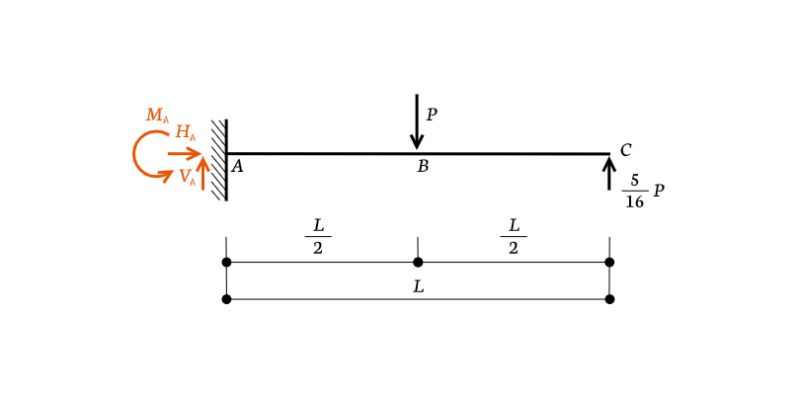
ほかの反力も求める

ここまで来ればあとは点$A$側の反力を求めるだけです。断面力図を求める流れも全く同じですね。

力のつり合い式を立てて反力を求めると、

$$H_A = 0 , V_A = \frac{11}{16} P , M_A = \frac{3}{16} PL$$

という答えが出てくるはずです。

最後に、ポイントだけおさらいしておきましょう。不静定構造の問題をたわみ公式を使って解く時に気をつけることは、

の3点です。この3点に気をつけて問題に挑んでみるとよいでしょう。

まとめ

お疲れ様でした。

今回の内容で、たわみ公式をいまひとつ覚えてなかったなという人は関連記事があるので、読んで復習してみてください。

それでは、また。